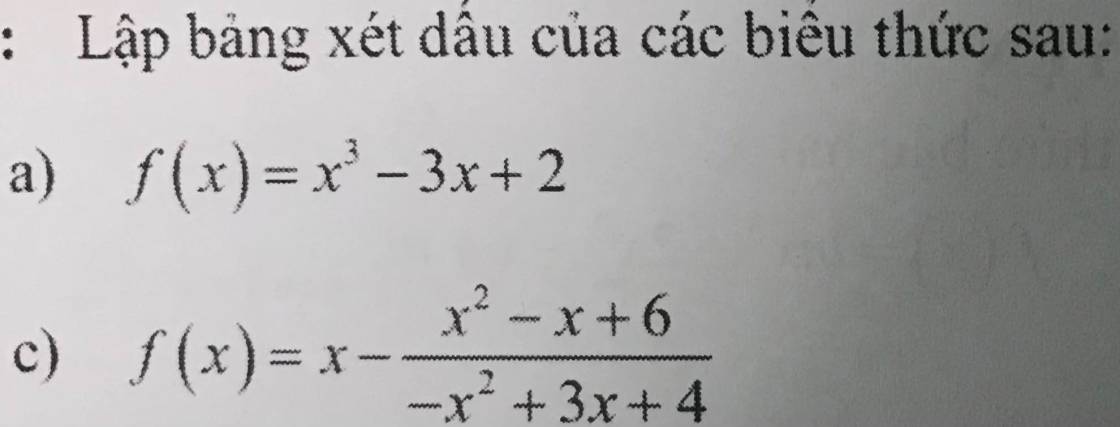a: \(f\left(x\right)=x^3-3x+2\)
\(=x^3-x-2x+2\)
\(=x\left(x-1\right)\left(x+1\right)-2\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x-2\right)\)
\(=\left(x+2\right)\left(x-1\right)^2\)
Đặt f(x)=0
=>\(\left(x+2\right)\left(x-1\right)^2=0\)
=>\(\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
Đặt x+2=0
=>x=-2
Vì x+2 có a=1>0 nên x+2>0 khi x>-2 và x+2<0 khi x<-2
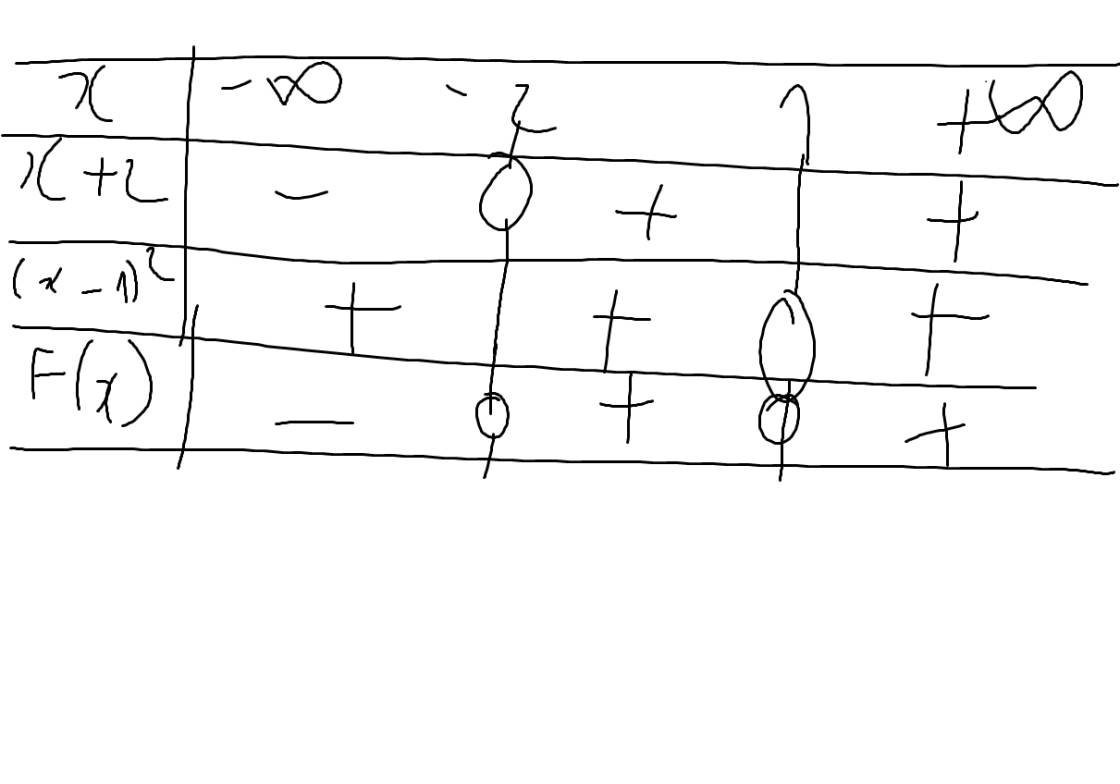
Bảng xét dấu:
c: \(f\left(x\right)=x-\dfrac{x^2-x+6}{-x^2+3x+4}\)
\(=\dfrac{x\left(-x^2+3x+4\right)-x^2+x-6}{-x^2+3x+4}\)
\(=\dfrac{-x^3+3x^2+4x-x^2+x-6}{-x^2+3x+4}\)
\(=\dfrac{-x^3+2x^2+5x-6}{-x^2+3x+4}\)
\(=\dfrac{x^3-2x^2-5x+6}{x^2-3x-4}\)
\(=\dfrac{x^3-3x^2+x^2-3x-2x+6}{\left(x-4\right)\left(x+1\right)}\)
\(=\dfrac{\left(x-3\right)\left(x^2+x-2\right)}{\left(x-4\right)\left(x+1\right)}\)
\(=\dfrac{\left(x-3\right)\left(x+2\right)\left(x-1\right)}{\left(x-4\right)\left(x+1\right)}\)
Đặt x-3=0
=>x=3
Đặt x+2=0
=>x=-2
Đặt x-1=0
=>x=1
Đặt x-4=0
=>x=4
Đặt x+1=0
=>x=-1
Bảng xét dấu: