Question

Answer 1

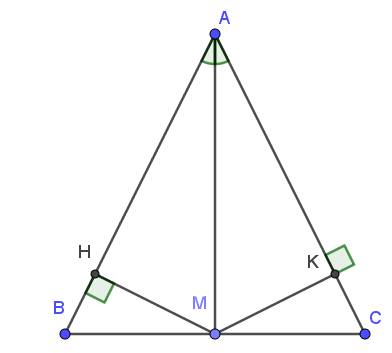
Lời giải:
a. Xét tam giác $ABM$ và $ACM$ có:

$AB=AC$

$BM=CM$ (do $M$ là trung điểm $BC$)

$AM$ chung

$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)

$\Rightarrow \widehat{AMB}=\widehat{AMC}$

Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$

$\Rightarrow \widehat{AMB}=\widehat{AMC}=90^0$

$\Rightarrow AM\perp BC$

b.

Xét tam giác $MHB$ và $MKC$ có:

$MB=MC$ (do $M$ là trung điểm $BC$)

$\widehat{MHB}=\widehat{MKC}=90^0$

$\widehat{MBH}=\widehat{ABC}=\widehat{ACB}=\widehat{MCK}$ (do $ABC$ cân tại $A$)

$\Rightarrow \triangle MHB=\triangle MKC$ (ch-gn)

Answer 2

Hình vẽ: