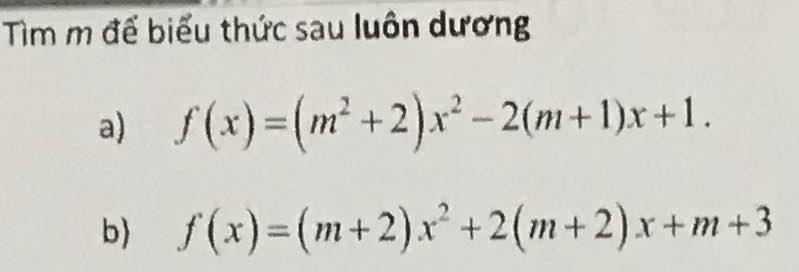a: \(f\left(x\right)=\left(m^2+2\right)x^2-2\left(m+1\right)x+1\)
\(\text{Δ}=\left[-2\left(m+1\right)\right]^2-4\cdot1\left(m^2+2\right)\)
\(=4\left(m+1\right)^2-4\left(m^2+2\right)\)
\(=4\left(m^2+2m+1-m^2-2\right)\)
\(=4\left(2m-1\right)\)
Để f(x)>0 với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< 0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4\left(2m-1\right)< 0\\m^2+2>0\left(luônđúng\right)\end{matrix}\right.\)
=>2m-1<0
=>2m<1
=>\(m< \dfrac{1}{2}\)
b: TH1: m=-2
\(f\left(x\right)=\left(-2+2\right)x^2+2\left(-2+2\right)+\left(-2\right)+3\)
=-2+3
=1>0
=>Nhận
TH2: m<>-2
\(\text{Δ}=\left[2\left(m+2\right)\right]^2-4\left(m+2\right)\left(m+3\right)\)
\(=4\left(m^2+4m+4\right)-4\left(m^2+5m+6\right)\)
\(=4m^2+16m+16-4m^2-20m-24=-4m-8\)
Để f(x)>0 với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< 0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-4m-8< 0\\m+2>0\end{matrix}\right.\)
=>\(m>-2\)
Vậy: m>=-2