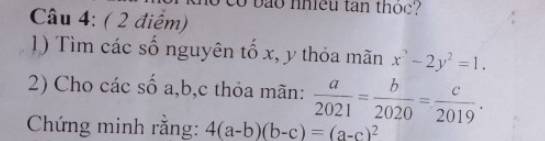1.
Do \(2y^2\) luôn chẵn \(\Rightarrow x^2-1\) chẵn \(\Rightarrow x\) lẻ
Đặt \(x=2k+1\)
\(\Rightarrow\left(2k+1\right)^2-1=2y^2\)
\(\Leftrightarrow4k^2+4k=2y^2\)
\(\Leftrightarrow y^2=2\left(k^2+k\right)\)
\(\Rightarrow y^2\) chẵn \(\Rightarrow y\) chẵn
Mà y là SNT \(\Rightarrow y=2\)
\(\Rightarrow x^2=2y^2+1=9\Rightarrow x=3\) (thỏa mãn)
2.
Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{a}{2021}=\dfrac{b}{2020}=\dfrac{c}{2019}=\dfrac{a-b}{2021-2020}=\dfrac{b-c}{2020-2019}=\dfrac{a-c}{2021-2019}\)
\(\Rightarrow a-b=b-c=\dfrac{a-c}{2}\)
\(\Rightarrow2\left(a-b\right)=2\left(b-c\right)=a-c\)
\(\Rightarrow\left(a-c\right)^2=2.\left(a-b\right).2\left(b-c\right)=4\left(a-b\right)\left(b-c\right)\)