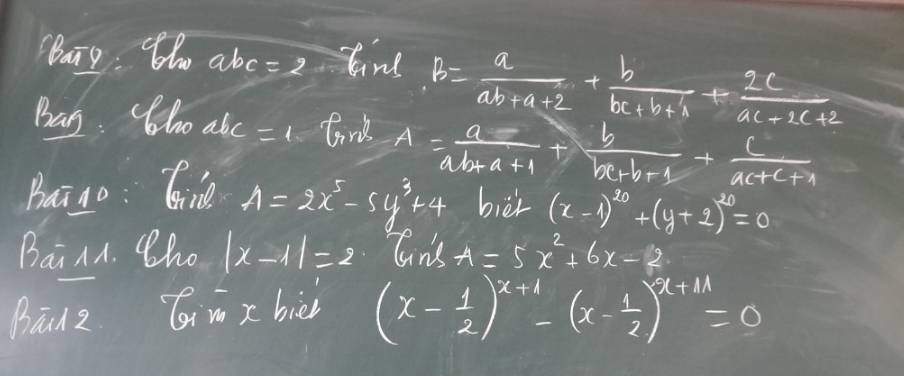Bài 10:
\(\left(x-1\right)^{20}>=0\forall x\)
\(\left(y+2\right)^{20}>=0\forall y\)
Do đó: \(\left(x-1\right)^{20}+\left(y+2\right)^{20}>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-1=0\\y+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(A=2x^5-5y^3+4\)
\(=2\cdot1^5-5\cdot\left(-2\right)^3+4\)
=6+40
=46
Bài 11:
|x-1|=2
=>\(\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
Thay x=3 vào A, ta được:
\(A=5\cdot3^2+6\cdot3-2=45+16=61\)
Thay x=-1 vào A, ta được:
\(A=5\cdot\left(-1\right)^2+6\cdot\left(-1\right)-2\)
=5-6-2
=-3
Đúng 2
Bình luận (0)
