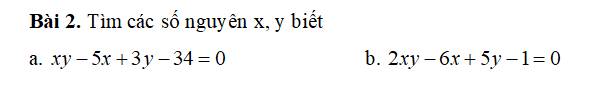a.
\(xy-5x+3y-34=0\)
\(\Leftrightarrow xy-5x+3y-15=19\)
\(\Leftrightarrow x\left(y-5\right)+3\left(y-5\right)=19\)
\(\Leftrightarrow\left(x+3\right)\left(y-5\right)=19\)
Ta có bảng:
| x+3 | -19 | -1 | 1 | 19 |
| y-5 | -1 | -19 | 19 | 1 |
| x | -22 | -4 | -2 | 16 |
| y | 4 | -14 | 24 | 6 |
Vậy \(\left(x;y\right)=\left(-22;4\right);\left(-4;-14\right);\left(-2;24\right);\left(16;6\right)\)
b.
\(2xy-6x+5y-15=-14\)
\(\Leftrightarrow2x\left(y-3\right)+5\left(y-3\right)=-14\)
\(\Leftrightarrow\left(2x+5\right)\left(y-3\right)=-14\)
Do 2x+5 luôn lẻ nên ta chỉ cần xét các cặp ước của -14 mà 2x+5 nhận giá trị lẻ.
Ta có bảng:
| 2x+5 | -7 | -1 | 1 | 7 |
| y-3 | 2 | 14 | -14 | -2 |
| x | -6 | -3 | -2 | 1 |
| y | 5 | 17 | -11 | 1 |
Vậy \(\left(x;y\right)=\left(-6;5\right);\left(-3;17\right);\left(-2;-11\right);\left(1;1\right)\)
a) \(xy-5x+3y-34=0\)
\(\Rightarrow x\left(y-5\right)+3y-15-19=0\)
\(\Rightarrow x\left(y-5\right)+3\left(y-5\right)=19\)
\(\Rightarrow\left(y-5\right)\left(x+3\right)=19\)
Ta có bảng:
| x + 3 | 1 | 19 | -1 | -19 |
| y - 5 | 19 | 1 | -19 | -1 |
| x | -2 | 16 | -4 | -22 |
| y | 24 | 6 | -14 | 4 |
b) \(2xy-6x+5y-1=0\)
\(\Rightarrow2x\left(y-3\right)+5y-15+14=0\)
\(\Rightarrow2x\left(y-3\right)+5\left(y-3\right)=-14\)
\(\Rightarrow\left(2x+5\right)\left(y-3\right)=-14\)
Do x nguyên nên 2x + 5 luôn là số lẻ
Ta có bảng:
| 2x + 5 | 1 | -1 | 7 | -7 |
| y - 3 | -14 | 14 | -2 | 2 |
| x | -2 | -3 | 1 | -6 |
| y | -11 | 17 | 1 | 5 |