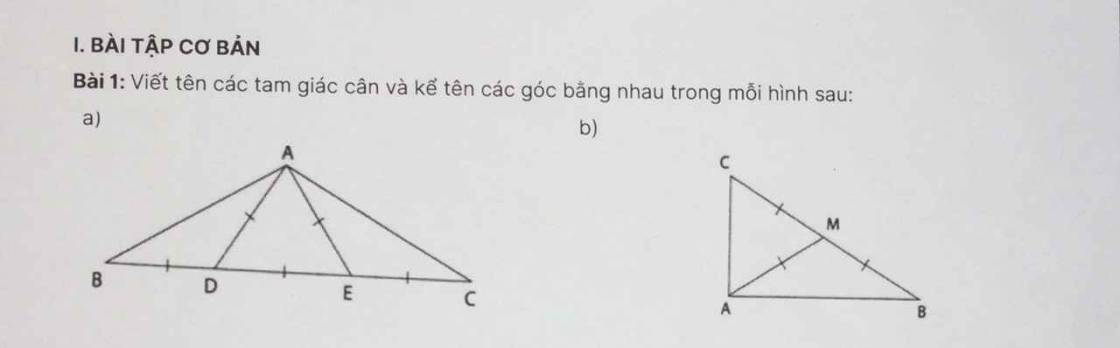
a: Xét ΔADE có AD=AE
nên ΔADE cân tại A
Xét ΔDAB có DA=DB
nên ΔDAB cân tại D
Xét ΔEAC có EA=EC
nên ΔEAC cân tại E
Ta có: \(\widehat{ADE}+\widehat{ADB}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{AEC}=180^0\)(hai góc kề bù)
mà \(\widehat{ADE}=\widehat{AED}\)
nên \(\widehat{ADB}=\widehat{AEC}\)
Xét ΔADB và ΔAEC có
AD=AE
\(\widehat{ADB}=\widehat{AEC}\)
DB=EC(=DE)
Do đó: ΔADB=ΔAEC
=>\(\widehat{ABD}=\widehat{ACE};\widehat{BAD}=\widehat{CAE}\)
mà \(\widehat{DAB}=\widehat{DBA}\)
nên \(\widehat{ABD}=\widehat{ACE}=\widehat{BAD}=\widehat{CAE}\)
b: Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
=>\(\widehat{MAB}=\widehat{MBA}\)
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}\)