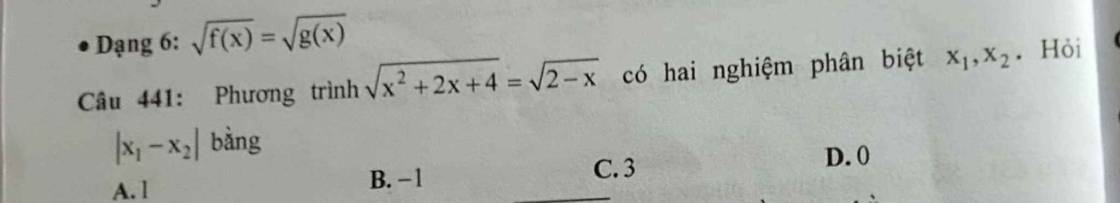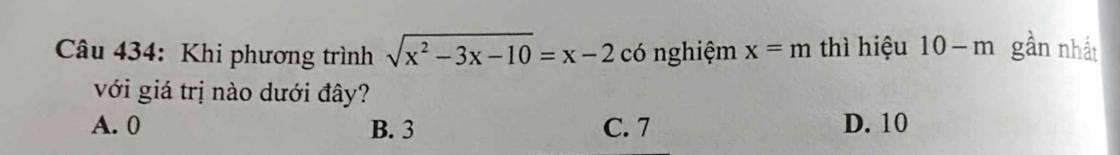Câu 441: \(\sqrt{x^2+2x+4}=\sqrt{2-x}\left(dkxd:x\ge2\right)\)
\(\Leftrightarrow\left|x^2+2x+4\right|=\left|2-x\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+2x+4=2-x\\x^2+2x+4=x-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+3x+2=0\\x^2-x+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=-1\\x_2=-2\end{matrix}\right.\) \(\left(tmdk\right)\)
\(\left|x_1-x_2\right|=\left|-1-\left(-2\right)\right|=\left|1\right|=1\)
Câu 434: \(\sqrt{x^2-3x-10}=x-2\)
\(dkxd:D=(-\infty;-2]\cup[5;+\infty)\)
\(\Leftrightarrow\left|x^2-3x-10\right|=x-2\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-10=x^2-4x+2\\-x^2+3x+10=x^2-4x+2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=12\\-2x^2+7x+8=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=12\left(tm\right)\\\left\{{}\begin{matrix}x=\dfrac{7+\sqrt{113}}{4}\left(ktm\right)\\x=\dfrac{7-\sqrt{113}}{4}\left(ktm\right)\end{matrix}\right.\end{matrix}\right.\)
Thay giá trị \(x=m\) vào \(10-m\)
\(\Leftrightarrow10-12=-2\)
Chọn A