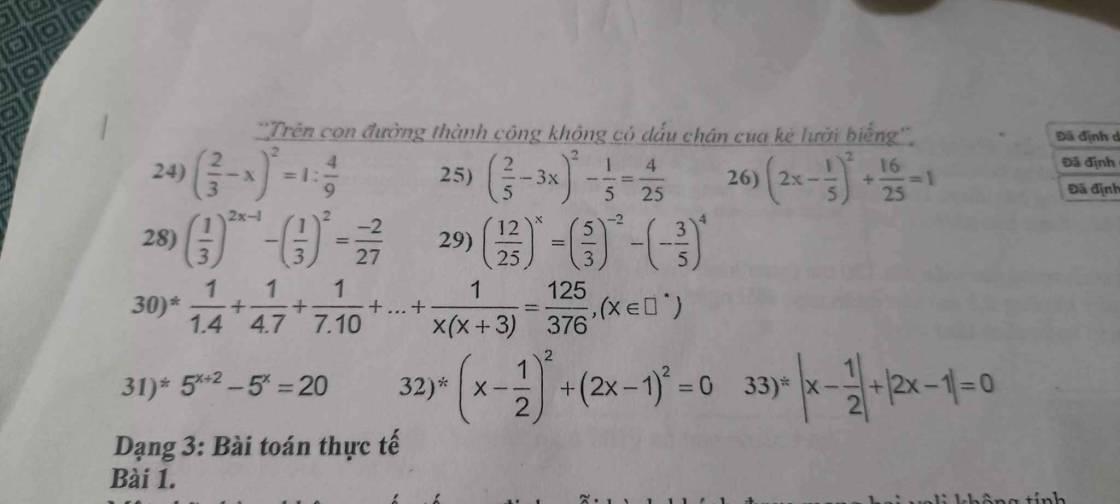24: \(\left(\dfrac{2}{3}-x\right)^2=1:\dfrac{4}{9}\)
=>\(\left(x-\dfrac{2}{3}\right)^2=1\cdot\dfrac{9}{4}=\dfrac{9}{4}\)
=>\(\left[{}\begin{matrix}x-\dfrac{2}{3}=\dfrac{3}{2}\\x-\dfrac{2}{3}=-\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}+\dfrac{3}{2}=\dfrac{13}{6}\\x=-\dfrac{3}{2}+\dfrac{2}{3}=\dfrac{-9+4}{6}=-\dfrac{5}{6}\end{matrix}\right.\)
25: \(\left(\dfrac{2}{5}-3x\right)^2-\dfrac{1}{5}=\dfrac{4}{25}\)
=>\(\left(3x-\dfrac{2}{5}\right)^2=\dfrac{4}{25}+\dfrac{1}{5}=\dfrac{9}{25}\)
=>\(\left[{}\begin{matrix}3x-\dfrac{2}{5}=\dfrac{3}{5}\\3x-\dfrac{2}{5}=-\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=1\\3x=-\dfrac{1}{5}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-\dfrac{1}{15}\end{matrix}\right.\)
26: \(\left(2x-\dfrac{1}{5}\right)^2+\dfrac{16}{25}=1\)
=>\(\left(2x-\dfrac{1}{5}\right)^2=1-\dfrac{16}{25}=\dfrac{9}{25}\)
=>\(\left[{}\begin{matrix}2x-\dfrac{1}{5}=\dfrac{3}{5}\\2x-\dfrac{1}{5}=-\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{4}{5}\\2x=-\dfrac{2}{5}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{2}{5}\\x=-\dfrac{1}{5}\end{matrix}\right.\)
28: \(\left(\dfrac{1}{3}\right)^{2x-1}-\left(\dfrac{1}{3}\right)^2=-\dfrac{2}{27}\)
=>\(\left(\dfrac{1}{3}\right)^{2x-1}=-\dfrac{2}{27}+\left(\dfrac{1}{3}\right)^2=\dfrac{1}{9}-\dfrac{2}{27}=\dfrac{1}{27}\)
=>2x-1=3
=>2x=4
=>x=2
29: \(\left(\dfrac{12}{25}\right)^x=\left(\dfrac{5}{3}\right)^{-2}-\left(-\dfrac{3}{5}\right)^4\)
=>\(\left(\dfrac{12}{25}\right)^x=\dfrac{9}{25}-\dfrac{81}{625}=\dfrac{144}{625}\)
=>x=2
30: \(\dfrac{1}{1\cdot4}+\dfrac{1}{4\cdot7}+...+\dfrac{1}{x\left(x+3\right)}=\dfrac{125}{376}\)
=>\(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+...+\dfrac{3}{x\left(x+3\right)}=\dfrac{375}{376}\)
=>\(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{x}-\dfrac{1}{x+3}=\dfrac{375}{376}\)
=>\(1-\dfrac{1}{x+3}=\dfrac{375}{376}\)
=>\(\dfrac{1}{x+3}=1-\dfrac{375}{376}=\dfrac{1}{376}\)
=>x+3=376
=>x=373(nhận)
31: \(5^{x+2}-5^x=20\)
=>\(5^x\cdot25-5^x=20\)
=>\(5^x\cdot24=20\)
=>\(5^x=\dfrac{20}{24}=\dfrac{5}{6}\)
=>\(x=log_5\left(\dfrac{5}{6}\right)=1-log_56\)