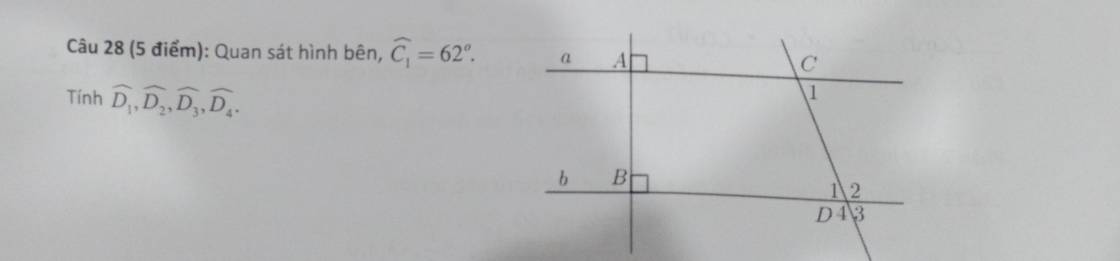
Ta có: a\(\perp\)AB
b\(\perp\)AB
Do đó: a//b
Ta có: a//b
=>\(\widehat{D_1}=\widehat{C_1}\)(hai góc so le trong)
mà \(\widehat{C_1}=62^0\)
nên \(\widehat{D_1}=62^0\)
Ta có: \(\widehat{D_1}+\widehat{D_2}=180^0\)(hai góc kề bù)
=>\(\widehat{D_2}+62^0=180^0\)
=>\(\widehat{D_2}=180^0-62^0=118^0\)
Ta có: \(\widehat{D_1}=\widehat{D_3}\)(hai góc đối đỉnh)
mà \(\widehat{D_1}=62^0\)
nên \(\widehat{D_3}=62^0\)
Ta có: \(\widehat{D_2}=\widehat{D_4}\)(hai góc đối đỉnh)
mà \(\widehat{D_2}=118^0\)
nên \(\widehat{D_4}=118^0\)
góc D1=C1=62o ( hai góc so le trong )
D1+D2=180o ( hai góc kề bù )
62o+D2=180o
D2= 180o - 62o
D2 =118o
góc D1=D3= 62o ( hai góc đối đỉnh )
góc D4= D2=118o ( hai góc đối đỉnh )