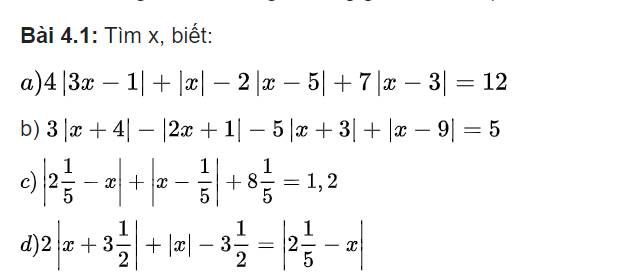a: \(4\left|3x-1\right|+\left|x\right|-2\left|x-5\right|+7\left|x-3\right|=12\)(1)
TH1: x<0
Phương trình (1) sẽ trở thành:
\(4\left(1-3x\right)-x-2\left(5-x\right)+7\left(3-x\right)=12\)
=>\(4-12x-x-10+2x+21-7x=12\)
=>\(-18x+15=12\)
=>-18x=-3
=>\(x=\dfrac{1}{6}\left(loại\right)\)
TH2: \(0< =x< \dfrac{1}{3}\)
Phương trình (1) sẽ trở thành:
\(4\left(1-3x\right)+x-2\left(5-x\right)+7\left(3-x\right)=12\)
=>\(4-12x+x-10+2x+21-7x=12\)
=>-16x+15=12
=>-16x=-3
=>\(x=\dfrac{3}{16}\)(nhận)
TH3: \(\dfrac{1}{3}< =x< 3\)
Phương trình (1) sẽ trở thành:
\(4\left(3x-1\right)+x-2\left(5-x\right)+7\left(3-x\right)=12\)
=>\(12x-4+x-10+2x+21-7x=12\)
=>\(8x+7=12\)
=>8x=5
=>\(x=\dfrac{5}{8}\left(nhận\right)\)
TH4: 3<=x<5
Phương trình (1) sẽ trở thành:
\(4\left(3x-1\right)+x-2\left(5-x\right)+7\left(x-3\right)=12\)
=>12x-4+x-10+2x+7x-21=12
=>22x-35=12
=>22x=47
=>\(x=\dfrac{47}{22}\left(loại\right)\)
TH5: x>=5
Phương trình (1) sẽ trở thành:
\(4\left(3x-1\right)+x-2\left(x-5\right)+7\left(x-3\right)=12\)
=>12x-4+x-2x+10+7x-21=12
=>18x-15=12
=>18x=27
=>x=1,5(loại)
b: \(3\left|x+4\right|-\left|2x+1\right|-5\left|x+3\right|+\left|x-9\right|=5\left(2\right)\)
TH1: x<-4
Phương trình (2) sẽ trở thành:
\(3\left(-x-4\right)-\left(-2x-1\right)-5\left(-x-3\right)+9-x=5\)
=>\(-3x-12+2x+1+5x+15+9-x=5\)
=>3x+13=5
=>3x=-8
=>x=-8/3(loại)
TH2: \(-4< =x< -3\)
Phương trình (2) sẽ trở thành:
\(3\left(x+4\right)-\left(-2x-1\right)-5\left(-x-3\right)+9-x=5\)
=>3x+12+2x+1+5x+15+9-x=5
=>9x+37=5
=>9x=-32
=>\(x=-\dfrac{32}{9}\left(nhận\right)\)
TH3: -3<=x<-1/2
Phương trình (2) sẽ trở thành:
\(3\left(x+4\right)-\left(-2x-1\right)-5\left(x+3\right)+9-x=5\)
=>3x+12+2x+1-5x-15+9-x=5
=>-x+7=5
=>-x=-2
=>x=2(nhận)
TH4: -1/2<=x<9
Phương trình (2) sẽ trở thành:
\(3\left(x+4\right)-\left(2x+1\right)-5\left(x+3\right)+9-x=5\)
=>3x+12-2x-1-5x-15+9-x=5
=>-5x+5=5
=>-5x=0
=>x=0(nhận)
TH5: x>=9
Phương trình (2) sẽ trở thành: \(3\left(x+4\right)-\left(2x+1\right)-5\left(x+3\right)+x-9=5\)
=>3x+12-2x-1-5x-15+x-9=5
=>-5x-13=5
=>-5x=18
=>x=-18/5(loại)
c: \(\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+8\dfrac{1}{5}=1,2\)
=>\(\left|x-\dfrac{11}{5}\right|+\left|x-\dfrac{1}{5}\right|=1,2-8,2=-7< 0\)
mà \(\left|x-\dfrac{11}{5}\right|+\left|x-\dfrac{1}{5}\right|>=0\forall x\)
nên \(x\in\varnothing\)
d: \(2\left|x+3\dfrac{1}{2}\right|+\left|x\right|-3\dfrac{1}{2}=\left|2\dfrac{1}{5}-x\right|\)
=>\(2\left|x+3,5\right|+\left|x\right|-\left|x-2,2\right|=3,5\left(3\right)\)
TH1: x<-3,5
Phương trình (3) sẽ trở thành \(2\left(-x-3,5\right)-x-\left(2,2-x\right)=3,5\)
=>-2x-7-x-2,2+x=3,5
=>-2x-9,2=3,5
=>-2x=3,5+9,2=12,7
=>x=-12,7/2=-6,35(nhận)
TH2: -3,5<=x<0
Phương trình (3) sẽ trở thành:
\(2\left(x+3,5\right)+\left(-x\right)-\left(2,2-x\right)=3,5\)
=>2x+7-x-2,2+x=3,5
=>2x+4,8=3,5
=>2x=-1,3
=>x=-0,65(nhận)
TH3: 0<=x<2,2
Phương trình (3) sẽ trở thành:
\(2\left(x+3,5\right)+x-\left(2,2-x\right)=3,5\)
=>2x+7+x-2,2+x=3,5
=>4x+4,8=3,5
=>4x=-1,3
=>x=-0,325(loại)
TH4: x>=2,2
Phương trình (3) sẽ trở thành:
\(2\left(x+3,5\right)+x-\left(x-2,2\right)=3,5\)
=>2x+7+x-x+2,2=3,5
=>2x+9,2=3,5
=>2x=3,5-9,2=-5,7
=>x=-57/20(loại)