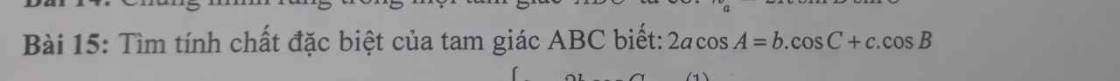Xét ΔABC có
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
\(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
\(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
\(2a\cdot cosA=b\cdot cosC+c\cdot cosB\)
=>\(2\cdot BC\cdot\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=AC\cdot\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}+AB\cdot\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(\dfrac{BC\left(AB^2+AC^2-BC^2\right)}{AB\cdot AC}=\dfrac{CA^2+CB^2-AB^2}{2\cdot CB}+\dfrac{BA^2+BC^2-AC^2}{2\cdot CB}\)
=>\(BC\cdot\dfrac{\left(AB^2+AC^2-BC^2\right)}{AB\cdot AC}=\dfrac{CA^2+CB^2-AB^2+BA^2+BC^2-AC^2}{2\cdot CB}\)
=>\(BC\cdot\dfrac{AB^2+AC^2-BC^2}{AB\cdot AC}=\dfrac{2BC^2}{2BC}=BC\)
=>\(AB^2+AC^2-BC^2=AB\cdot AC\)
=>\(BC^2=AB^2+AC^2-AB\cdot AC\)
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(AB^2+AC^2=2\cdot AB\cdot AC\cdot cosA+BC^2\)
=>\(2\cdot AB\cdot AC\cdot cosA+BC^2-AB\cdot AC=BC^2\)
=>\(2\cdot AB\cdot AC\cdot cosA-AB\cdot AC=0\)
=>\(AB\cdot AC\left(2cosA-1\right)=0\)
=>\(cosA=\dfrac{1}{2}\)
=>\(\widehat{A}=60^0\)