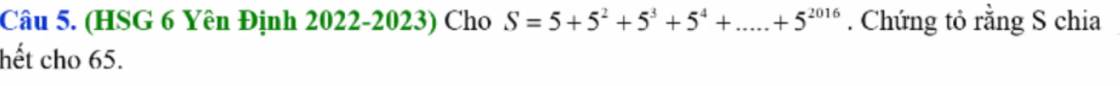\(S=5+5^2+5^3+...+5^{2016}\)
\(=\left(5+5^2+5^3+5^4\right)+\left(5^5+5^6+5^7+5^8\right)...+5^{2012}\left(5+5^2+5^3+5^4\right)\)
\(=\left(5+5^2+5^3+5^4\right)+5^4\left(5+5^2+5^3+5^4\right)+...+5^{2012}\left(5+5^2+5^3+5^4\right)\)
\(=780\left(1+5^4...+5^{2012}\right)\)
\(=65\cdot12\cdot\left(1+5^4+...+5^{2012}\right)⋮65\)
S = 5 + 5² + 5³ + ... + 5²⁰¹⁶
= (5 + 5² + 5³ + 5⁴) + (5⁵ + 5⁶ + 5⁷ + 5⁸ + ... + (5²⁰¹³ + 5²⁰¹⁴ + 5²⁰¹⁵ + 5²⁰¹⁶)
= 780 + 5⁴.(5 + 5² + 5³ + 5⁴) + ... + 5²⁰¹².(5 + 5² + 5³ + 5⁴)
= 780 + 5⁴.780 + ... + 5²⁰¹².780
= 780.(1 + 5⁴ + ... + 5²⁰¹²)
= 65.12.(1 + 5⁴ + ... + 5²⁰¹²) ⋮ 65
Vậy S ⋮ 65