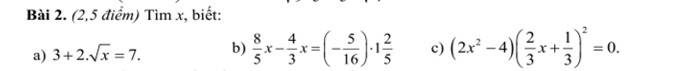a: ĐKXĐ: x>=0
\(2\sqrt{x}+3=7\)
=>\(2\sqrt{x}=4\)
=>\(\sqrt{x}=2\)
=>x=4(nhận)
b: \(\dfrac{8}{5}x-\dfrac{4}{3}x=\left(-\dfrac{5}{16}\right)\cdot\left(1\dfrac{2}{5}\right)\)
=>\(x\left(\dfrac{8}{5}-\dfrac{4}{3}\right)=\dfrac{-5}{16}\cdot\dfrac{7}{5}=-\dfrac{7}{16}\)
=>\(x\cdot\dfrac{24-20}{15}=\dfrac{-7}{16}\)
=>\(x\cdot\dfrac{4}{15}=-\dfrac{7}{16}\)
=>\(x=-\dfrac{7}{16}:\dfrac{4}{15}=\dfrac{-7}{16}\cdot\dfrac{15}{4}=-\dfrac{105}{64}\)
c: \(\left(2x^2-4\right)\left(\dfrac{2}{3}x+\dfrac{1}{3}\right)^2=0\)
=>\(\left[{}\begin{matrix}2x^2-4=0\\\dfrac{2}{3}x+\dfrac{1}{3}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x^2=2\end{matrix}\right.\)
=>\(x\in\left\{-\dfrac{1}{2};\sqrt{2};-\sqrt{2}\right\}\)
`#3107.101107`
a)
`3+ 2 \sqrt{x} = 7`
`=> 2\sqrt{x} = 7 - 3`
`=> 2 \sqrt{x} = 5`
`=> \sqrt{x} = 5/2`
`=> x = (5/2)^2`
`=> x = 25/4`
Vậy, `x = 25/4`
b)
`8/5x - 4/3x = (-5/16) * 1 2/5`
`=> 4/15 x = -7/16`
`=> x = -7/16 \div 4/15`
`=> x = -105/64`
Vậy, `x = -105/64`
c)
`(2x^2 - 4)(2/3x + 1/3)^2 = 0`
`=>`\(\left[{}\begin{matrix}2x^2-4=0\\\left(\dfrac{2}{3}x+\dfrac{1}{3}\right)^2=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}2x^2=4\\\dfrac{2}{3}x+\dfrac{1}{3}=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x^2=2\\\dfrac{2}{3}x=-\dfrac{1}{3}\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\pm\sqrt{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Vậy, `x \in {-1/2; - \sqrt{2}; \sqrt{2}}.`