Question

Answer 1

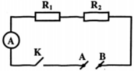
\(R_1=\rho_1\dfrac{l_1}{S_1}\Rightarrow S_1=\dfrac{\rho_1\cdot l_1}{R_1}\)

\(R_2=\rho_2\dfrac{l_2}{S_2}\Rightarrow S_2=\dfrac{\rho_2\cdot l_2}{R_2}\)

Để so sánh 2 tiết diện của dây ta có biểu thức: 

\(\dfrac{S_1}{S_2}=\dfrac{\rho_1\cdot\dfrac{l_2}{R_2}}{\rho_2\cdot\dfrac{l_2}{R_2}}\) (Mà: \(l_1=l_2;R_1=R_2\Rightarrow\dfrac{l_1}{R_1}=\dfrac{l_2}{R_2}\))

\(\Rightarrow\dfrac{S_1}{S_2}=\dfrac{\rho_1}{\rho_2}=\dfrac{1,7\cdot10^{-8}}{2,8\cdot10^{-8}}=\dfrac{1,7}{2,8}=\dfrac{17}{28}\)

\(\Rightarrow28S_1=17S_2\)

\(\Rightarrow S_2>S_1\)