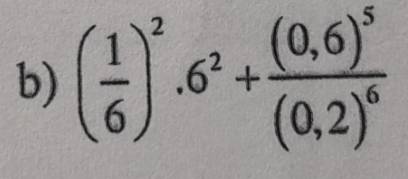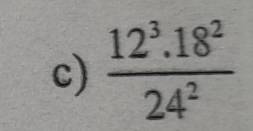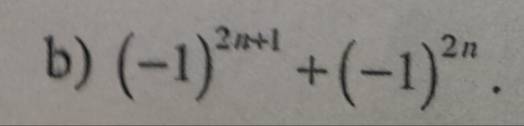Question

Answer 1

a: \(2^6\cdot3^3=\left(2^2\cdot3\right)^3=12^3\)

b: \(6^4\cdot8^2=8^2\cdot36^2=\left(8\cdot36\right)^2=288^2\)

c: \(16\cdot81=2^4\cdot3^4=6^4\)

b: \(\left(\dfrac{1}{6}\right)^2\cdot6^2+\dfrac{0.6^5}{0.2^6}\)

\(=\left(\dfrac{1}{6}\cdot6\right)^2+\dfrac{0.2^5\cdot0.3^5}{0.2^5\cdot0.2}\)

\(=1+0.3^5\cdot5=1.01215\)

c: \(\dfrac{12^3\cdot18^2}{24^2}=\dfrac{\left(2^2\cdot3\right)^3\cdot\left(3^2\cdot2\right)^2}{\left(2^3\cdot3\right)^2}\)

\(=\dfrac{2^6\cdot3^3\cdot3^4\cdot2^2}{2^6\cdot3^2}=3^5\cdot2^2=972\)

b: \(\left(-1\right)^{2n+1}+\left(-1\right)^{2n}\)

=-1+1

=0