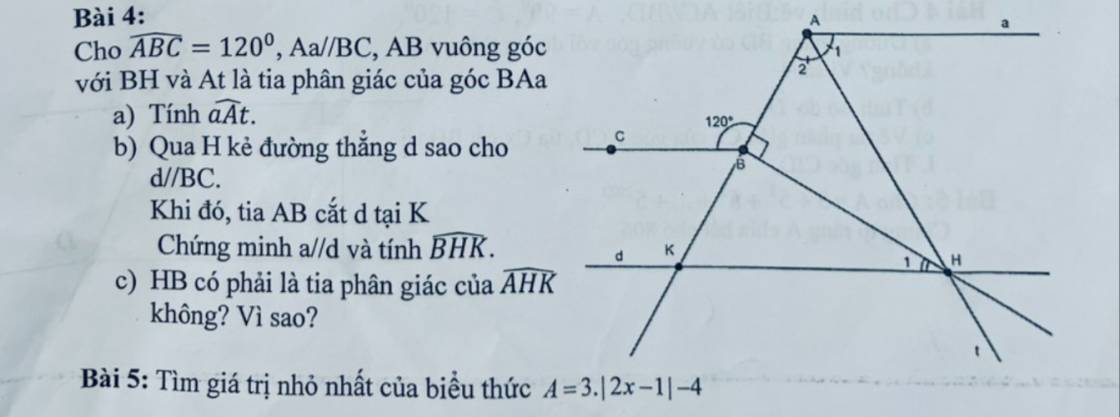
a: Aa//BC
=>\(\widehat{aAB}=\widehat{ABC}\)(hai góc so le trong)
=>\(\widehat{aAB}=120^0\)
At là phân giác của \(\widehat{aAB}\)
=>\(\widehat{aAt}=\dfrac{120^0}{2}=60^0\)
b: d//BC
BC//a
Do đó: d//a
\(\widehat{CBH}+\widehat{CBA}+\widehat{ABH}=360^0\)
=>\(\widehat{CBH}=360^0-120^0-90^0=150^0\)
BC//d
=>\(\widehat{CBH}+\widehat{BHK}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{BHK}=30^0\)
c: d//a
=>\(\widehat{AHK}=\widehat{aAH}\)(hai góc so le trong)
=>\(\widehat{AHK}=60^0\)
\(\widehat{BHK}=\dfrac{1}{2}\cdot\widehat{AHK}\)
HB nằm giữa HA và HK
Do đó: HB là tia phân giác của \(\widehat{AHK}\)