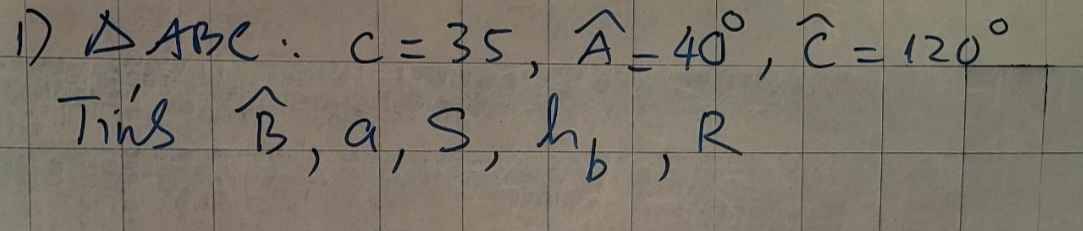Ta có: \(\widehat{B}=180^o-40^o-120^o=20^o\)
Theo định lý sin ta có:
\(\dfrac{AB}{sinC}=\dfrac{BC}{sinA}\)
\(\Rightarrow BC=\dfrac{AB\cdot sinA}{sinC}\)
\(\Rightarrow a=\dfrac{c\cdot sinA}{sinC}=\dfrac{35\cdot sin40^o}{sin120^o}\approx26\)
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}\)
\(\Rightarrow AC=b=\dfrac{AB\cdot sinB}{sinC}=\dfrac{35\cdot sin20^o}{sin120^o}\approx14\)
\(\Rightarrow S_{ABC}=AB\cdot AC\cdot\dfrac{1}{2}\cdot sinA=b\cdot c\cdot\dfrac{1}{2}\cdot sinA=14\cdot35\cdot\dfrac{1}{2}\cdot sin40^o\approx158\)
Ta có: \(p=\dfrac{a+b+c}{2}=\dfrac{35+26+14}{2}=\dfrac{75}{2}\)
Theo công thức Hê-rông ta có:
\(h_b=2\cdot\dfrac{\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}}{b}=2\cdot\dfrac{\sqrt{\dfrac{75}{2}\cdot\left(\dfrac{75}{2}-26\right)\cdot\left(\dfrac{75}{2}-14\right)\cdot\left(\dfrac{75}{2}-35\right)}}{14}=22\)
Ta có: \(S_{ABC}=\dfrac{abc}{4R}\)
\(\Rightarrow R=\dfrac{abc}{4S_{ABC}}=\dfrac{35\cdot14\cdot26}{4\cdot158}=20\)