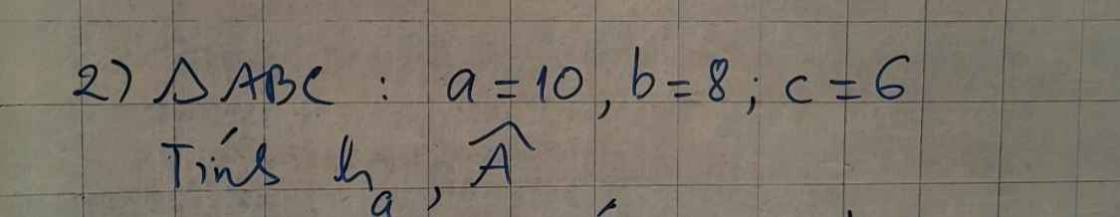Áp dung công thức Hê-rông:
\(S_{ABC}=\sqrt[]{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
mà \(p=\dfrac{a+b+c}{2}=\dfrac{10+8+6}{2}=12\)
\(\Leftrightarrow S_{ABC}=\sqrt[]{12\left(12-10\right)\left(12-8\right)\left(12-6\right)}\)
\(\Leftrightarrow S_{ABC}=\sqrt[]{12.2.4.6}=24\)
Ta lại có \(S_{ABC}=\dfrac{1}{2}.h_a.a\)
\(\Leftrightarrow h_a=\dfrac{2.S_{ABC}}{a}\)
\(\Leftrightarrow h_a=\dfrac{2.24}{10}=\dfrac{24}{5}\)
\(S_{ABC}=\dfrac{1}{2}bcsin\widehat{A}\)
\(\Leftrightarrow sin\widehat{A}=\dfrac{2.S_{ABC}}{bc}\)
\(\Leftrightarrow sin\widehat{A}=\dfrac{2.24}{8.6}=1\)
\(\Leftrightarrow\widehat{A}=90^o\)
Đúng 3
Bình luận (0)
