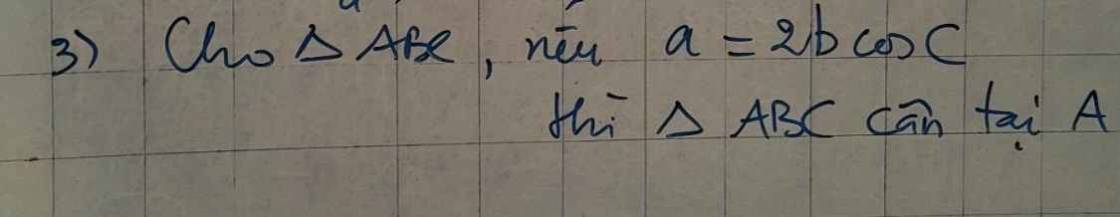Áp dụng định lý Cosin cho \(\Delta ABC\) ta có :
\(c^2=a^2+b^2-2abCosC\)
\(\Leftrightarrow cosC=\dfrac{a^2+b^2-c^2}{2ab}\)
Ta lại có : \(a=2bcosC\) (đề bài)
\(\Leftrightarrow a=2b.\dfrac{a^2+b^2-c^2}{2ab}\)
\(\Leftrightarrow a=\dfrac{a^2+b^2-c^2}{a}\)
\(\Leftrightarrow a^2=a^2+b^2-c^2\left(a>0\right)\)
\(\Leftrightarrow b^2=c^2\)
\(\Leftrightarrow b=c\left(b;c>0\right)\)
Vậy \(\Delta ABC\) cân tại \(A\) \(\left(dpcm\right)\)