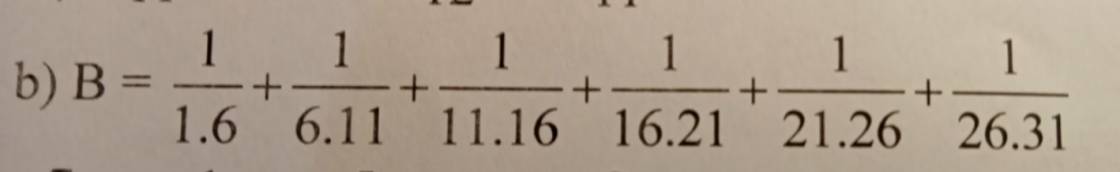\(B=\dfrac{1}{1\cdot6}+\dfrac{1}{6\cdot11}+\dfrac{1}{11\cdot16}+\dfrac{1}{16\cdot21}+\dfrac{1}{21\cdot26}+\dfrac{1}{26\cdot31}\)
\(=\dfrac{1}{5}\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+\dfrac{5}{11\cdot16}+\dfrac{5}{16\cdot21}+\dfrac{5}{21\cdot26}+\dfrac{5}{26\cdot31}\right)\)
\(=\dfrac{1}{5}\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{26}-\dfrac{1}{31}\right)\)
\(=\dfrac{1}{5}\left(1-\dfrac{1}{31}\right)\)
\(=\dfrac{1}{5}\cdot\dfrac{30}{31}=\dfrac{6}{31}\)
Đúng 2
Bình luận (0)
