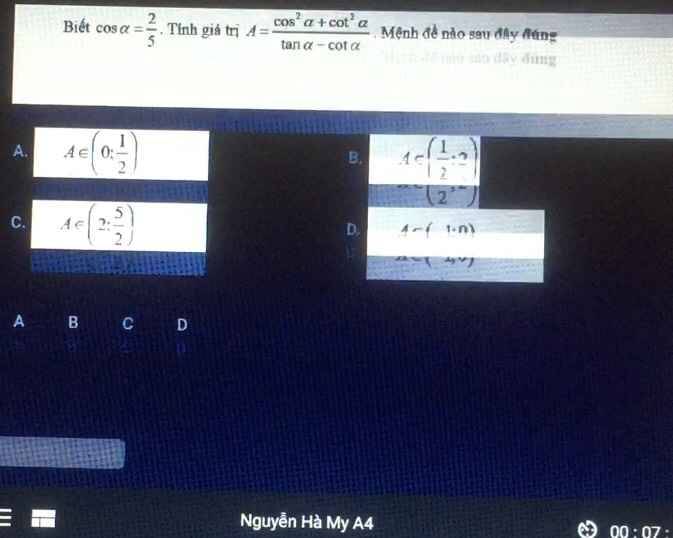
Xét trên tử số: \(M=cos^2\alpha+cot^2\alpha\)
Ta sẽ có: \(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\). Thật vậy, nhân cả 2 vế cho \(sin^2\alpha\) ta được:
\(sin^2\alpha\left(1+\dfrac{cos^2\alpha}{sin^2\alpha}\right)=1\)
\(\Leftrightarrow sin^2\alpha+cos^2\alpha=1\) (đúng).
Trở lại với hệ thức, ta sẽ có:
\(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\Leftrightarrow cot^2\alpha=\dfrac{1}{sin^2\alpha}-1=\dfrac{1}{1-cos^2\alpha}-1\).Thay \(cos\alpha=\dfrac{2}{5}\Rightarrow cot^2\alpha=\dfrac{4}{21}\).
\(\Rightarrow M=\dfrac{184}{525}\).
Xét dưới mẫu số: \(N=tan\alpha-cot\alpha\)
\(=\dfrac{sin\alpha}{cos\alpha}-\dfrac{cos\alpha}{sin\alpha}\)
\(=\dfrac{sin^2\alpha-cos^2\alpha}{sin\alpha.cos\alpha}-\dfrac{1-2cos^2\alpha}{cos\alpha\sqrt{1-cos^2\alpha}}=\dfrac{17\sqrt{21}}{42}\)
\(\Rightarrow A=\dfrac{M}{N}\approx0,19\)
Chọn A.