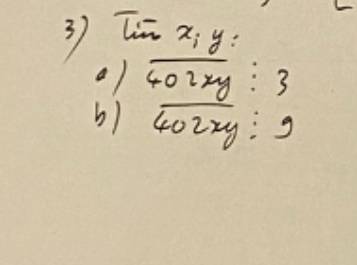a: =>x+y chia hết cho 3
=>x+y=3k(k∈N)
b: =>x+y chia hểt cho 9
=>x+y=9k(k∈N)
a) Để \(402xy⋮3\) thì tổng của chúng phải chia hết cho 3
Ta xét : 4 + 0 + 2 = 6 \(⋮3\)
Vậy x = 0 ; y = 3 để 40203 chia hết cho 3
=> còn nhiều trường hợp khác nhưng mình chọn trường hợp này để có thể chia hết cho cả phần b) nữa nhé bạn
b) Để \(402xy⋮9\) thì tổng của chúng phải chia hết cho 9
Như mình nói ở trên x = 0 ; y = 9 vì 40203 = 4 + 0 + 2 + 0+ 3 = 9 chia cho 9
x,y là chữ số => 0 ≤ x,y < 10; x,y∈N
a) Để 402xy chia hết cho 3 thì 4+0+2+x+y chia hết cho 3
=> 6+x+y chia hết cho 3
=> x+y chia hết cho 3
=> (x,y) = (0,0); (1,2); (2,1); (3,0); (0,3); ...
b) Để 402xy chia hết cho 9 thì 4+0+2+x+y chia hết cho 9
=> 6+x+y chia hết cho 9
=> x+y chia 9 dư 3
=> (x,y) = (0,3); (1,2); (3,0); (2,1); ...