`@` `\text {Ans}`
`\downarrow`
`2,`
`a,`
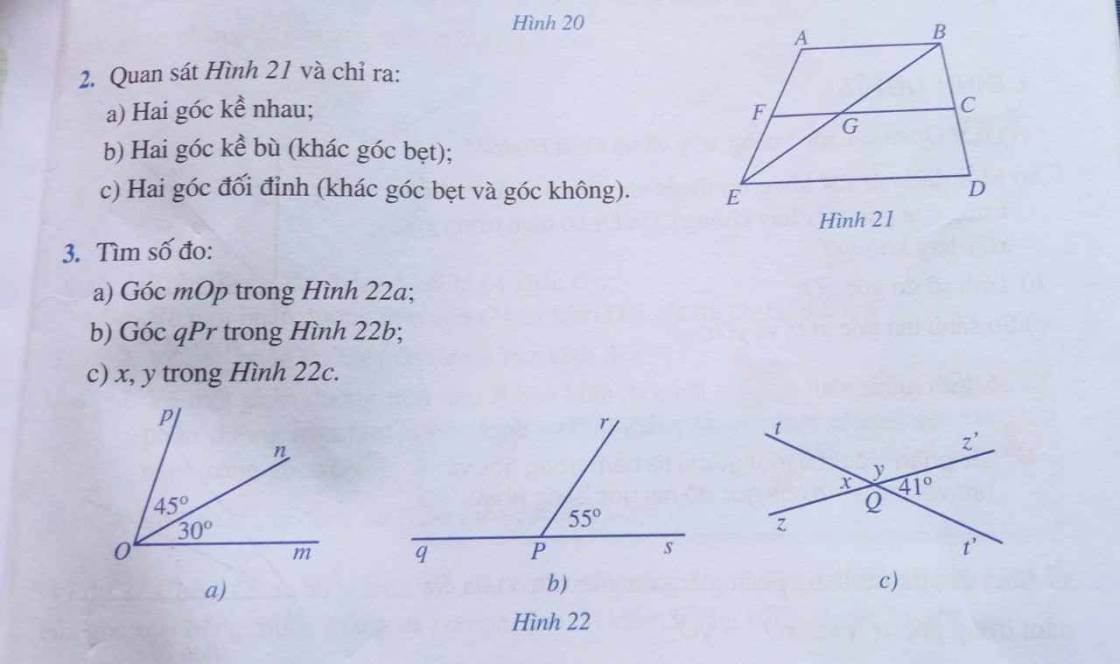
$\widehat {ABE}$ và $\widehat {DBE}$
$\widehat {AEB}$ và $\widehat {DEB}$
`b,`
$\widehat {AFC}$ và $\widehat {EFC}$
$\widehat {BCF}$ và $\widehat {DCF}$
`c,`
$\widehat {FGE}$ và $\widehat {BGC}$
`3,`
`a,`
Ta có: $\widehat {mOp} = \widehat {mOn} + \widehat {pOn}$
`->` $\widehat {mOp} = 30^0 + 45^0$
`->` $\widehat {mOp} = 75^0$
Vậy, $\widehat {mOp} = 75^0$
`b,`
Vì $\widehat {qPr}$ và $\widehat {sPr}$ là `2` góc kề bù
`->` $\widehat {qPr}+\widehat {sPr} = 180^0$
`->` $\widehat {qPr} + 55^0 = 180^0$
`->` $\widehat {qPr} = 125^0$
Vậy, $\widehat {qPr} = 125^0$
`c,`
Vì $\widehat {t'Qz'}$ và $\widehat {zQt}$ là `2` góc đối đỉnh
`=>` $\widehat {tQz} = 41^0$
Vì $\widehat {t'Qz'}$ và $\widehat {tQz'}$ là `2` góc kề bù
`=>` $\widehat {tQz'} + \widehat {t'Qz'} = 180^0$
`=>` $\widehat {tQz'} + 41^0 = 180^0$
`=>` $\widehat {tQz'} = 139^0$
Vì $\widehat {tQz'}$ và $\widehat {t'Qz}$ là `2` góc đối đỉnh
`=>` $\widehat {tQz'} = \widehat {t'Qz} = 139^0$