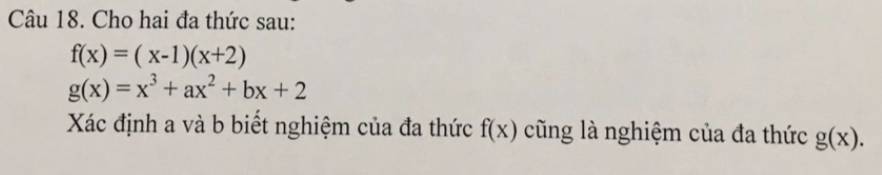\(f\left(x\right)=\left(x-1\right)\left(x+2\right)\)
\(f\left(x\right)=0\)
\(\left(x-1\right)\left(x+2\right)=0\)
\(x-1=0\) hoặc \(x+2=0\)
*) \(x-1=0\)
\(x=1\)
*) \(x+2=0\)
\(x=-2\)
Vậy \(x=-2;x=1\) là nghiệm của \(f\left(x\right)\)
Do nghiệm của \(f\left(x\right)\) cũng là nghiệm của \(g\left(x\right)\) nên \(x=-2;x=1\) là nghiệm của \(g\left(x\right)\)
\(\Rightarrow g\left(-2\right)=g\left(1\right)=0\)
*) \(g\left(-2\right)=0\)
\(\Rightarrow\left(-2\right)^3+a.\left(-2\right)^2+b.\left(-2\right)+2=0\)
\(\Rightarrow4a-2b-6=0\) (1)
*) \(g\left(1\right)=0\)
\(\Rightarrow1^3+a.1^2+b.1+2=0\)
\(\Rightarrow a+b+3=0\)
\(\Rightarrow a=-b-3\) thay vào (1), ta được:
\(4.\left(-b-3\right)-2b-6=0\)
\(-4b-12-2b-6=0\)
\(-6b-18=0\)
\(-6b=18\)
\(b=-3\)
\(\Rightarrow a=-\left(-3\right)-3\)
\(=0\)
Vậy \(a=0;b=-3\)