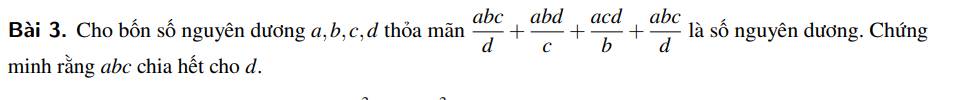Question

Answer 1

Đặt \(x=\dfrac{abc}{d}+\dfrac{bcd}{a}=\dfrac{bc\left(a^2+d^2\right)}{ad}\)

\(y=\dfrac{cda}{b}+\dfrac{dab}{c}=\dfrac{ad}{bc}\left(b^2+c^2\right)\)

x+y nguyên

=>(x+y)^2=x^2+y^2+2xy thuộc Z

mà \(x\cdot y=\left(a^2+d^2\right)\left(b^2+c^2\right)\)

xy nguyên

=>x^2+y^2 nguyên

=>x,y nguyen

=>abc/d+bcd/a nguyên

mà abc/d*bcd/a=(bc)^2 nguyên

nên abc/d nguyên

=>abc chia hết cho d