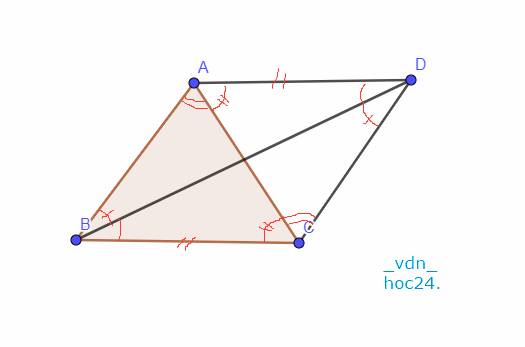
`a,`
Vì `\text {AB // CD, AD//BC (gt)}`
`->`\(\widehat{DAC}=\widehat{BCA}, \widehat{BAC}=\widehat{DCA}, \widehat{ADB}=\widehat{CBD}, \widehat{ABD}=\widehat{CDB}\) `(\text {tính chất 2 đường thẳng //})`
Xét Tam giác `ABC` và Tam giác `CDA` có:
\(\widehat{DAC}=\widehat{BCA} (CMT)\)
`\text {AC chung}`
\(\widehat{BAC}=\widehat{DCA} (CMT)\)
`=> \text {Tam giác ABC = Tam giác CDA (g-c-g)}`
`b,` Vì Tam giác `ABC =` Tam giác `CDA (a)`
`-> AD = BC (\text {2 cạnh tương ứng})`
Xét Tam giác `AMD` và Tam giác `CMB` có:
\(\widehat{BCM}=\widehat{DAM} (CMT)\)
`AD = BC (CMT)`
\(\widehat{MBC}=\widehat{MDA} (CMT)\)
`=> \text {Tam giác AMD = Tam giác CMB (g-c-g)}`
`-> MA = MC (\text {2 cạnh tương ứng})`
`-> \text {M là trung điểm của AC (đpcm)}`