Question

Answer 1

    

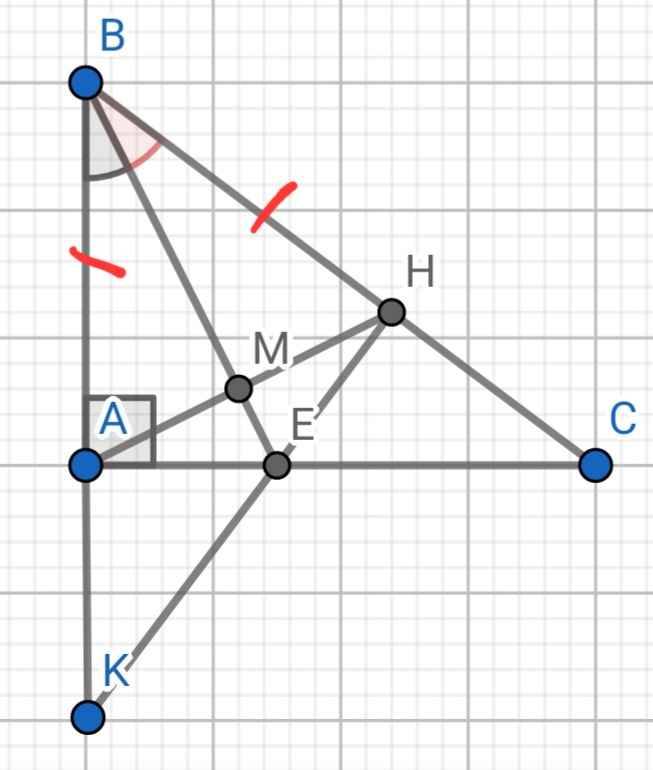
a) Xét ∆ABE và ∆HBE có:

BE chung

∠ABE = ∠HBE (BE là tia phân giác của ABC)

BA = BH (gt)

⇒ ∆ABE = ∆HBE (c-g-c)

⇒ ∠BAE = ∠BHE (hai góc tương ứng)

⇒ BHE = 90⁰

⇒ EH ⊥ BC

b) Gọi M là giao điểm của BE và AH

Xét ∆ABM và ∆HBM có:

BA = BH (gt)

∠ABM = ∠HBM (BE là phân giác của ABC)

BM chung

⇒ ∆ABM = ∆HBM (c-g-c)

⇒ ∠BMA = ∠BMH (hai góc tương ứng)

Mà BMA và BMH kề bù

⇒ ∠BMA = ∠BMH = 180⁰ : 2 = 90⁰

⇒ BM ⊥ AH   (1)

Do ∆ABM = ∆HBM (cmt)

⇒ AM = HM (hai cạnh tương ứng)

⇒ M là trung điểm AH  (2)

Từ (1) và (2) ⇒ BM là đường trung trực của AH

c) Do ∆ABE = ∆HBE (cmt)

⇒ AE = HE (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆AKE và ∆HCE có:

AE = HE (cmt)

∠AEK = ∠HEC (đối đỉnh)

⇒ ∆AKE = ∆HCE (cạnh góc vuông - góc nhọn kề)