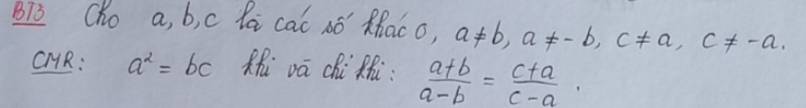Question

Answer 1

\(\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\)

\(\Leftrightarrow\left(a+b\right)\left(c-a\right)=\left(a-b\right)\left(c+a\right)\)

\(\Leftrightarrow ac-a^2+bc-ab=ac+a^2-bc-ab\)

\(\Leftrightarrow-2a^2+2bc=0\)

\(\Leftrightarrow-2\left(a^2-bc\right)=0\)

\(\Leftrightarrow a^2-bc=0\)

\(\Leftrightarrow a^2=bc\left(dpcm\right)\)

Vậy \(a^2=bc\) khi và chỉ khi \(\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\)