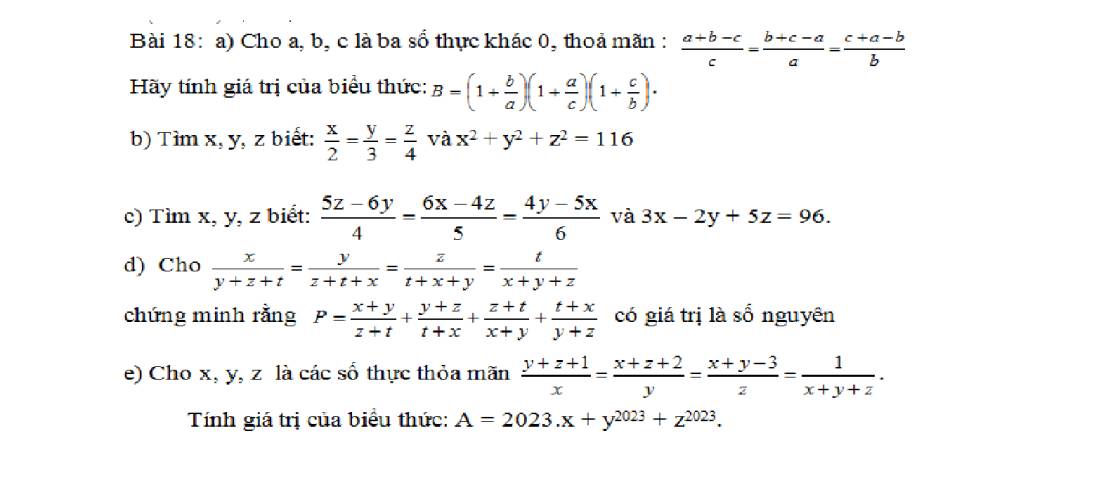18.a
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a+b-c}{c}=\frac{b+c-a}{a}=\frac{c+a-b}{b}=\frac{a+b-c+b+c-a+c+a-b}{c+a+b}=\frac{a+b+c}{a+b+c}=1$
$\Rightarrow a+b-c=c; b+c-a=a; c+a-b=b$
$\Rightarrow a+b=2c; b+c=2a; c+a=2b$
Do đó:
\(B=(1+\frac{b}{a})(1+\frac{a}{c})(1+\frac{c}{b})=\frac{(a+b)(b+c)(c+a)}{abc}=\frac{(2c)(2a)(2b)}{abc}=\frac{8abc}{abc}=8\)
18.b
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=k$
$\Rightarrow x=2k; y=3k; z=4k$
$\Rightarrow x^2+y^2+z^2=(2k)^2+(3k)^2+(4k)^2=116$
$\Rightarrow 29k^2=116$
$\Rightarrow k^2=4\Rightarrow k=2$ hoặc $k=-2$
Với $k=2$ thì $x=2k=4; y=3k=6; z=4k=8$
Với $k=-2$ thì $x=2k=-4; y=3k=-6; z=4k=-8$