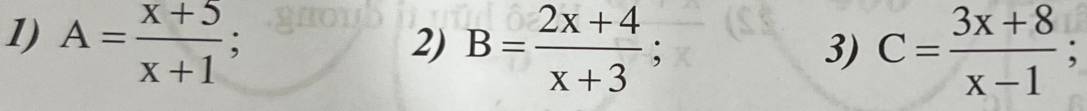Question

Answer 1

a) \(A=\dfrac{x+5}{x+1}=1+\dfrac{4}{x+1}\)

Để \(A\in Z\Rightarrow\left(x+1\right)\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)

\(\Rightarrow x\in\left\{0;-2;1;-3;3;-5\right\}\)

b) \(B=\dfrac{2x+4}{x+3}=\dfrac{2\left(x+3\right)-2}{x+3}=2-\dfrac{2}{x+3}\)

Để \(B\in Z\Rightarrow\left(x+3\right)\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)

\(\Rightarrow x\in\left\{-2;-4;-1;-5\right\}\)

c) \(C=\dfrac{3x+8}{x-1}=\dfrac{3\left(x-1\right)+11}{x-1}=3+\dfrac{11}{x-1}\)

Để \(C\in Z\Rightarrow\left(x-1\right)\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)

\(\Rightarrow x\in\left\{2;0;12;-10\right\}\)