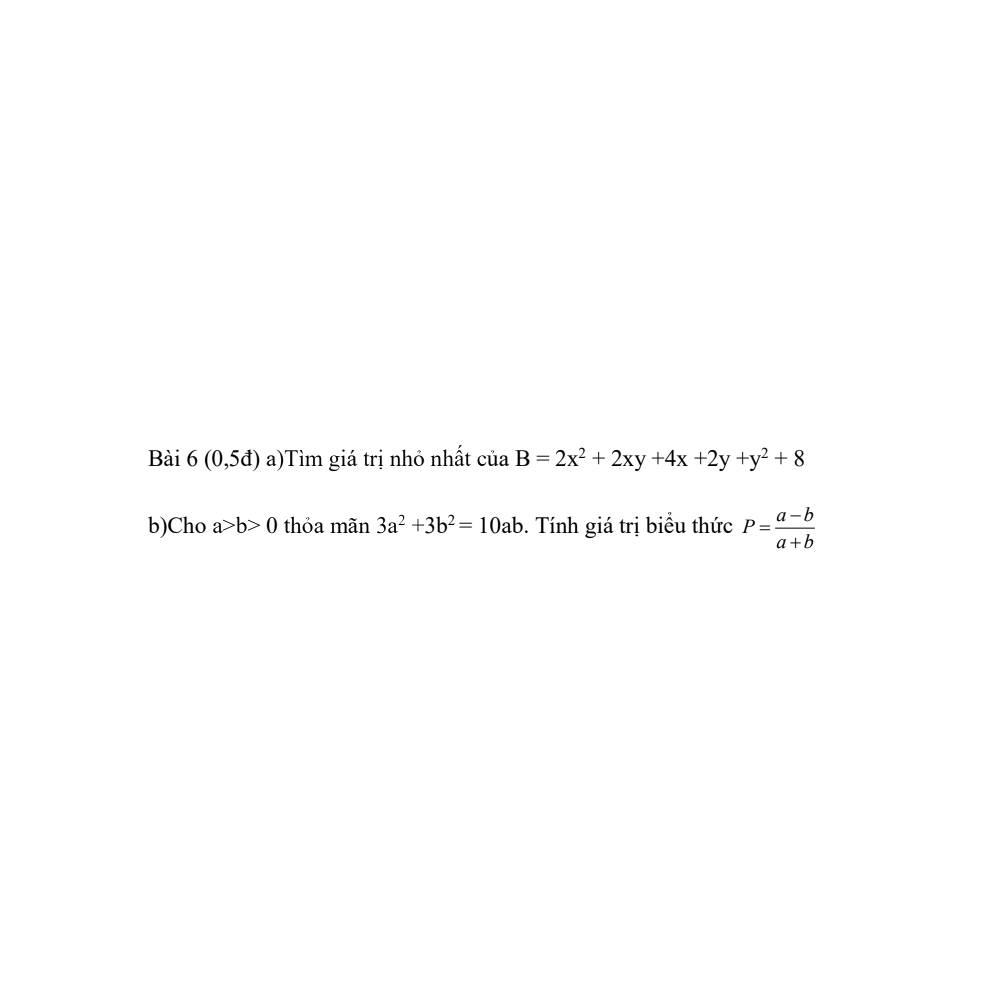a) \(B=2x^2+2xy+4x+2y+y^2+8\)
\(=\left(x^2+y^2+1+2xy+2y+2x\right)+\left(x^2+2x+1\right)+6\)
\(=\left(x+y+1\right)^2+\left(x+1\right)^2+6\ge6\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x+y+1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
Vậy \(MinB=6\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
b) Theo giả thiết, ta có:
\(3a^2+3b^2=10ab\)
\(\Leftrightarrow\left(3a^2-9ab\right)-\left(ab-3b^2\right)=0\)
\(\Leftrightarrow3a\left(a-3b\right)-b\left(a-3b\right)=0\)
\(\Leftrightarrow\left(3a-b\right)\left(a-3b\right)=0\)
\(\Leftrightarrow3a=b\) hoặc \(a=3b\)
Với \(3a=b,\) ta có: \(P=\dfrac{a-b}{a+b}=\dfrac{a-3a}{a+3a}=\dfrac{-2a}{4a}=-\dfrac{1}{2}\)
Với \(a=3b,\) ta có: \(P=\dfrac{a-b}{a+b}=\dfrac{3b-b}{3b+b}=\dfrac{2b}{4b}=\dfrac{1}{2}\)