Question

Answer 1

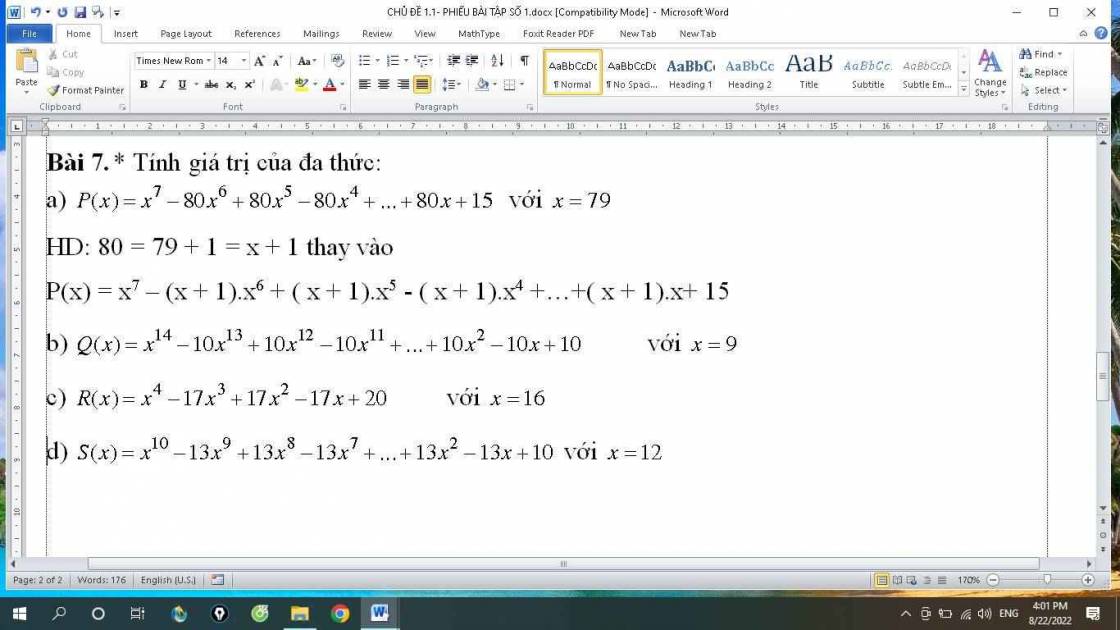
b, Ta có x = 9 => x + 1 = 10 

\(Q\left(x\right)=x^{14}-\left(x+1\right)x^{13}+\left(x+1\right)x^{12}-...+\left(x+1\right)x^2-10x+10\)

\(=x^{14}-x^{14}-x^{13}+x^{13}+x^{12}-...+x^3+x^2-10x+10\)

\(=x^2-10x+10=\left(x-5\right)^2-15\)

Thay vào ta được \(4^2-15=1\)

c, Ta có x = 16 <=> x + 1 = 17 

\(R\left(x\right)=x^4-\left(x+1\right)x^3+\left(x+1\right)x^2-\left(x+1\right)x+20\)

\(=x^4-x^4-x^3+x^3+x^2-x^2+x+20=x+20\)

Thay vào ta được = 16 + 20 = 36 

d, tương tự