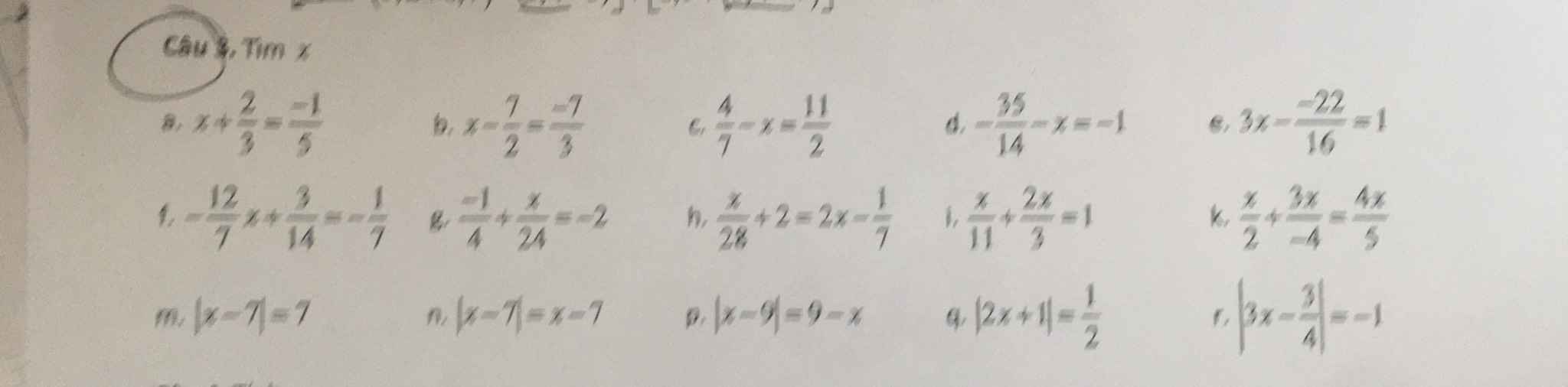\(a,x+\dfrac{2}{3}=\dfrac{-1}{5}\)
\(x=\dfrac{-1}{5}-\dfrac{2}{3}\)
\(x=\dfrac{-3-10}{15}=\dfrac{-13}{15}\)
\(b,x-\dfrac{7}{2}=\dfrac{-7}{3}\)
\(x=\dfrac{-7}{3}+\dfrac{7}{2}\)
\(x=\dfrac{-14+21}{6}=\dfrac{7}{6}\)
\(c,\dfrac{4}{7}-x=\dfrac{11}{2}\)
\(x=\dfrac{4}{7}-\dfrac{11}{2}\)
\(x=\dfrac{8-77}{14}=\dfrac{-69}{14}\)
\(d,-\dfrac{35}{14}-x=-1\)
\(x=-\dfrac{35}{14}-\left(-1\right)\)
\(x=\dfrac{\left(-35\right)-\left(-14\right)}{14}=\dfrac{-21}{14}=\dfrac{-3}{2}\)
\(e,3x-\dfrac{-22}{16}=1\)
\(3x=1+\dfrac{-22}{16}\)
\(3x=\dfrac{-3}{8}\)
\(x=\dfrac{-3}{8}:3\)
\(x=\dfrac{-3}{24}=\dfrac{-1}{8}\)
\(f,-\dfrac{12}{7}x+\dfrac{3}{14}=-\dfrac{1}{7}\)
\(-\dfrac{12}{7}x=-\dfrac{1}{7}-\dfrac{3}{14}\)
\(-\dfrac{12}{7}x=\dfrac{-5}{14}\)
\(x=\dfrac{-5}{14}:\dfrac{-12}{7}\)
\(x=\dfrac{-35}{-168}=\dfrac{-5}{-24}=\dfrac{5}{24}\)
\(g,\dfrac{-1}{4}+\dfrac{x}{24}=-2\)
\(\dfrac{x}{24}=-2-\dfrac{-1}{4}\)
\(\dfrac{x}{24}=\dfrac{-7}{4}\)
\(x:24=\dfrac{-7}{4}\)
\(x=\dfrac{-7}{4}.24\)
\(x=\dfrac{-168}{4}=-42\)
\(h,\dfrac{x}{28}+2=2x-\dfrac{1}{7}\)
\(x+56=56x-4\)
\(x+56x=-4-56\)
\(-55x=-60\)
\(x=-60:-55\)
\(x=\dfrac{-60}{-55}=\dfrac{12}{11}\)
\(h,\dfrac{x}{11}+\dfrac{2x}{3}=1\)
\(3x+22x=33\)
\(\left(3+22\right)x=33\)
\(25x=33\)
\(x=33:25\)
\(x=\dfrac{33}{25}\)
\(k,\dfrac{x}{2}+\dfrac{3x}{-4}=\dfrac{4x}{5}\)
\(\dfrac{x}{2}-\dfrac{3x}{4}=\dfrac{4x}{5}\)
\(10x-15x=16x\)
\(\left(10-15\right)x=16x\)
\(-5x=16x\)
\(-5x-16x=0\)
\(\left(-5-16\right)x=0\)
\(-21x=0\)
\(x=0:-21\)
\(x=0\)
\(m,\left|x-7\right|=7\)
\(x-7=7\) hoặc \(x-7=-7\)
\(x=14\) hoặc \(x=0\)
\(n,\left|x-7\right|=x-7\)
\(x-7\ge0\)
\(x\ge7\)
\(q,\left|2x+1\right|=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}\left|2x+1\right|=\dfrac{1}{2}\\\left|2x+1\right|=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x=\dfrac{1}{2}-1\\2x=-\dfrac{1}{2}-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x=\dfrac{-1}{2}\\2x=\dfrac{-3}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{-1}{2}:2\\x=\dfrac{-3}{2}:2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{-1}{4}\\x=\dfrac{-3}{4}\end{matrix}\right.\)
\(f,\left|3x-\dfrac{3}{4}\right|=-1\)
\(\Rightarrow\left\{{}\begin{matrix}\left|3x-\dfrac{3}{4}\right|=-1\\\left|3x-\dfrac{3}{4}\right|=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x=-1+\dfrac{3}{4}\\3x=1+\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x=-\dfrac{1}{4}\\3x=\dfrac{7}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{4}:3\\x=\dfrac{7}{4}:3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{12}\\x=\dfrac{7}{12}\end{matrix}\right.\)