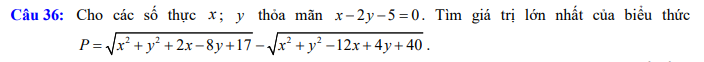Trên mặt phẳng tọa độ $Oxy$
Xét đường thẳng $d:x-2y-5=0$, điểm $I(-1;4)$, điểm $B(6;-2)$
Điểm $A(x;y) \in d$
Ta có: $\left\{\begin{matrix} \sqrt{(x+1)^2+(y-4)^2}=IA & \\ \sqrt{(x-6)^2+(y+2)^2}=AB & \end{matrix}\right.$
$\Leftrightarrow \sqrt{(x+1)^2+(y-4)^2}-\sqrt{(x-6)^2+(y+2)^2}=IA-AB(*)$
Gọi $B'$ là điểm đối xứng với $B$ qua $d$, $H$ là giao điểm của $BB'$ với $d$
Ta có $HB: 2x+y-10=0$
Tọa độ điểm $H$ là nghiệm của hệ phương trình: $\left\{\begin{matrix} x-2y-5=0 & \\ x+2y-10=0 & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=5 & \\ y=0& \end{matrix}\right.$
Vậy $H(5;0)$
Do đó tọa độ điểm $B'$ là nghiệm của hệ: $\left\{\begin{matrix} 5=\frac{x_{B'}+6}{2} & \\ 0=\frac{y_{B'}-2}{2} & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_{B'}= 4 & \\ y_{B'}=2 & \end{matrix}\right.$
$(*)\Leftrightarrow \sqrt{(x+1)^2+(y-4)^2}-\sqrt{(x-6)^2+(y+2)^2}=IA -AB'$
Theo bất đẳng thức tam giác ta có: $IA-AB'\le IB'$
Do đó: $ \sqrt{(x+1)^2+(y-4)^2}-\sqrt{(x-6)^2+(y+2)^2} \le IB'$
Ta có $IB'=\sqrt{(4+1)^2+(2-4)^2}=\sqrt{29}$
Vậy $GTLN=\sqrt{29}$
Dấu $"="$ xảy ra khi và chỉ chỉ: $I,B',A$ thẳng hàng hay $IB' \cap d=A$
$\Leftrightarrow \left\{\begin{matrix} x-2y-5=0 & \\ 2x+5y=18 & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{61}{9} & \\ y=\frac{8}{9}& \end{matrix}\right.$