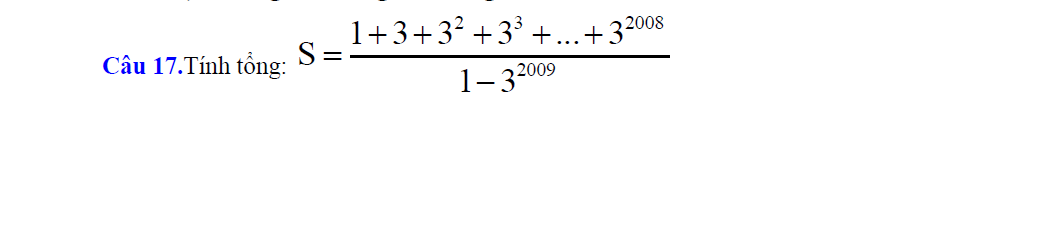Question

Answer 1

Đặt \(A=1+3+3^2+...+3^{2008}\)

\(A=\dfrac{3A-A}{2}=\dfrac{\left(3+3^2+3^3+...+3^{2009}\right)-\left(1+3+3^2+...+3^{2008}\right)}{2}\)

\(=\dfrac{3^{2009}-1}{2}\)

\(S=\dfrac{\dfrac{3^{2009}-1}{2}}{1-3^{2009}}=-\dfrac{1-3^{2009}}{2\left(1-3^{2009}\right)}=-\dfrac{1}{2}\)

Answer 2

Đặt `: S_1 = 1+3+.....+3^{2008}`

`=> 3S_1 = 3+3^2+.....+3^{2009}`

`=> 3S_1 - S_1 =(3+3^2+.....+3^{2009}) -( 1+3+.....+3^{2008})`

`=> 2S_1 = 3^{2009}-1`

`=> S_1=( 3^{2009}-1)/2`

`=> S = (( 3^{2009}-1)/2 )/( 1 - 3^{2009}) = -1/2`