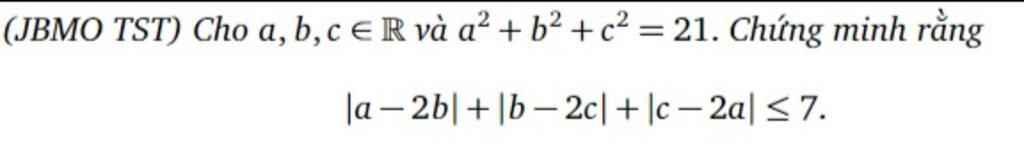Đăng đúng lớp nhé !
\(\text{#}T\)
\(P = | a − 2 b | + | b − 2 c | + | c − 2 a |\)
Giá trị lớn nhất là :
Xét \(a − 2 b ≥ 0 , b − 2 c ≥ 0 , c − 2 a < 0\), ta có :
\(P=3a-b-3c\text{≤}\sqrt{\left[3^2+\left(-1\right)^2+\left(-3\right)^2\right]\left[a^2+b^2+c^2\right]}\)
\(=\sqrt{19.21}=\sqrt{399}\)
\(\text{→}P\text{≤}\sqrt{399}\)
Tương tự với những trường hợp khác :
Chung quy lại , \(P ≤\)\(\sqrt{399}\) , dấu bằng xảy ra khi \(( a ; b ; c ) =\)\(\left(-3\sqrt{\dfrac{21}{19}};\sqrt{\dfrac{21}{19}};3\sqrt{\dfrac{21}{19}}\right)\) và các hoán vị
Giá trị nhỏ nhất :
\(P ^2 = ( a − 2 b ) ^2 + ( b − 2 c ) ^2 + ( c − 2 a ) ^2\)
\(+2 [ | ( a − 2 b ) ( b − 2 c ) | + | ( b − 2 c ) ( c − 2 a ) | + | ( c − 2 a ) ( a − 2 b ) | ]\)
\(≥ 5 ( a 2 + b 2 + c 2 ) − 4 ( a b + b c + c a )\)
\(+ 2 | ( a − 2 b ) ( b − 2 c ) + ( b − 2 c ) ( c − 2 a ) + ( c − 2 a ) ( a − 2 b ) |\)
\(= 105 − 4 ( a b + b c + c a ) + 2 ∣ − 2 ( a ^2 + b ^2 + c ^2 ) + 3 ( a b + b c + c a ) ∣\)
\(= 105 − 4 ( a b + b c + c a ) + 2 | 42 − 3 ( a b + b c + c a ) |\)
Xét \(42 − 3 ( a b + b c + c a ) ≥ 0 → a b + b c + c a ≤ 14\)
\(P ≥ 105 − 4 ( a b + b c + c a ) + 2 [ 42 − 3 ( a b + b c + c a ) ]\)
\(= 189 − 10 ( a b + b c + c a )\)
\(≥ 189 − 10.14\)
\(=49\)
\( P ≥ 7\)
Xét \(42 − 3 ( a b + b c + c a ) < 0 → a b + b c + c a > 14\)
\(P ≥ 105 − 4 ( a b + b c + c a ) + 2 [ 3 ( a b + b c + c a ) − 42 ]\)
\(= 21 + 2 ( a b + b c + c a ) \)
\(> 21 + 2.14\)
\(=49\)
\(P>7\)
Vậy \(P>7\) , dấu bằng xảy ra khi
\(\left\{{}\begin{matrix}a^2+b^2+c^2=21\\ab+bc+ca=14\\\left|\left(a-2b\right)\left(b-2c\right)\right|+\left|\left(b-2c\right)\left(c-2a\right)\right|+\left|\left(c-2a\right)\left(a-2b\right)\right|\\\text{| ( a − 2 b ) ( b − 2 c ) + ( b − 2 c ) ( c − 2 a ) + ( c − 2 a ) ( a − 2 b ) | }\end{matrix}\right.\)
\(( a ; b ; c ) = ( 4 ; 2 ; 1 )\) và các hoán vị hoặc \(c ( a ; b ; c ) = ( − 4 ; − 2 ; − 1 ) \)và các hoán vị