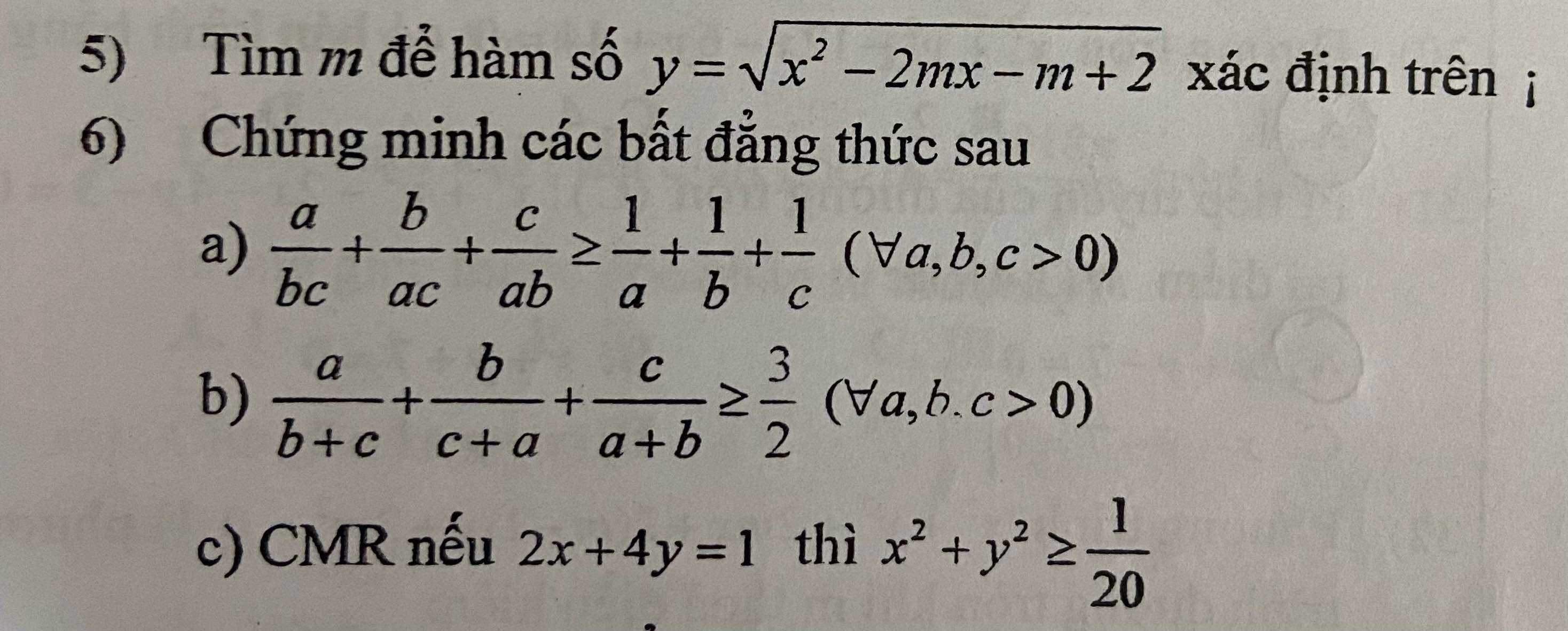5. H/s x/đ trên R \(\Leftrightarrow x^2-2mx-m+2\ge0\forall x\Leftrightarrow\Delta'\le0\)
\(\Leftrightarrow m^2-\left(2-m\right)\le0\Leftrightarrow m^2+m-2\le0\) \(\Leftrightarrow-2\le m\le1\)
6. a. Với a ; b ; c > 0 . AD BĐT Cauchy ta được : \(\dfrac{a}{bc}+\dfrac{b}{ac}\ge2\sqrt{\dfrac{a}{bc}.\dfrac{b}{ac}}=\dfrac{2}{c}\)
CMTT : \(\dfrac{b}{ac}+\dfrac{c}{ab}\ge\dfrac{2}{a};\dfrac{a}{bc}+\dfrac{c}{ab}\ge\dfrac{2}{b}\)
\(\Rightarrow2\left(\dfrac{a}{bc}+\dfrac{b}{ac}+\dfrac{c}{ab}\right)\ge2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\Rightarrow\dfrac{a}{bc}+\dfrac{b}{ac}+\dfrac{c}{ab}\ge\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
b. AD BĐT Cauchy ta được : \(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}=\dfrac{a^2}{ab+ac}+\dfrac{b^2}{bc+ba}+\dfrac{c^2}{ca+cb}\ge\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ac\right)}\ge\dfrac{3\left(ab+bc+ac\right)}{2\left(ab+bc+ac\right)}=\dfrac{3}{2}\)
c. AD BĐT B.C.S ta được : \(\left(2^2+4^2\right)\left(x^2+y^2\right)\ge\left(2x+4y\right)^2\Rightarrow20\left(x^2+y^2\right)\ge1\) \(\Rightarrow x^2+y^2\ge\dfrac{1}{20}\)
" = " \(\Leftrightarrow x=\dfrac{1}{10};y=\dfrac{1}{5}\)