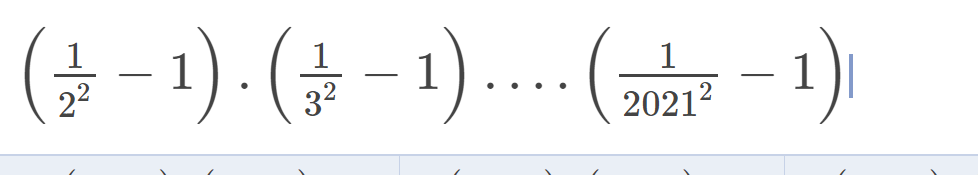Do tích đã cho có \(2021-2+1=2020\) nhân tử, là số chẵn nên:
\(\left(\dfrac{1}{2^2}-1\right)\left(\dfrac{1}{3^2}-1\right)...\left(\dfrac{1}{2021^2}-1\right)=\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)...\left(1-\dfrac{1}{2021^2}\right)\)
\(=\left(\dfrac{2^2-1}{2^2}\right)\left(\dfrac{3^2-1}{3^2}\right)...\left(\dfrac{2021^2-1}{2021^2}\right)\)
\(=\left(\dfrac{1.3}{2^2}\right)\left(\dfrac{2.4}{3^2}\right)...\left(\dfrac{2020.2022}{2021^2}\right)\)
\(=\left(\dfrac{1.2...2020}{2.3...2021}\right)\left(\dfrac{3.4...2022}{2.3...2021}\right)=\dfrac{1}{2021}.\dfrac{2022}{2}=\dfrac{1011}{2021}\)
Đúng 2
Bình luận (0)
