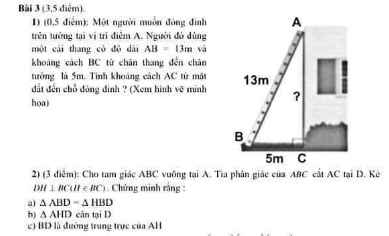
Bài 3.1 :
Xét \(\Delta ABC\) vuông tại A,
Theo định lí Pi-ta-go, ta có :
\(AB^2=BC^2+AC^2\)
\(\Rightarrow AC^2=AB^2-BC^2=13^2-5^2=144\)
\(\Rightarrow AC=\sqrt{144}=12\left(m\right)\)
Vậy khoảng cách AC từ mặt đất đến chỗ đóng định là \(12m\)
Bài 3.2 : (hình tự vẽ )
a, Xét \(\Delta ABD\) và \(\Delta HBD\) có :
\(\widehat{BAD}=\widehat{BHD}=90^0\)
\(\widehat{ABD}=\widehat{HBD}\left(BD\cdot là\cdot phân\cdot giác\cdot\widehat{ABC}\right)\)
\(BD:chung\)
\(\Rightarrow\Delta ABD=\Delta HBD\left(ch-gn\right)\)
b, Ta có : \(\Delta ABD=\Delta HBD\left(cmt\right)\)
\(\Rightarrow\widehat{HAD}=\widehat{AHD}\)
\(\Rightarrow\Delta HAD\cdot cân\cdot tại\cdot D\)
c, Gọi giao điểm của BD và AH là I
Xét \(\Delta ABI\) và \(\Delta HBI\) có :
\(AB=BH\left(\Delta ABD=\Delta HBD\right)\)
\(ABD=HBD\left(phân\cdot giác\cdot\widehat{ABC}\right)\)
\(BI:chung\)
\(\Rightarrow\Delta ABI=\Delta HBI\left(c-g-c\right)\)
\(\Rightarrow AI=IH\)
\(\Rightarrow I\cdot là\cdot trung\cdotđiểm\cdot của\cdot AH\cdot\left(1\right)\)
Ta có : \(\widehat{AIB}+\widehat{HBI}=180^0\)
Mà \(\widehat{AIB}=\widehat{HBI}\)
\(\Rightarrow\widehat{AIB}=\widehat{HBI}=90^0\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow BD\cdot là\cdotđường\cdot trung\cdot trực\cdot của\cdot AH\)