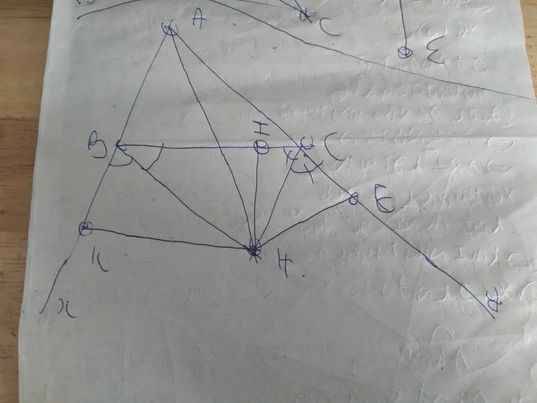
Gọi tam giác đề bài cho là ΔABC
Gọi Bx,Cy lần lượt là tia đối của tia BA và tia CA
=>\(\widehat{xBC}\) và \(\widehat{yCB}\) lần lượt là góc ngoài tại đỉnh B và đỉnh C của ΔABC
Kẻ tia phân giác của góc \(\widehat{xBC};\widehat{yCB}\), hai đường này cắt nhau tại H
Kẻ HI\(\perp\)BC tại I, HK\(\perp\)AB tại K; HE\(\perp\)AC tại E
=>HI,HK,HE lần lượt là khoảng cách từ H xuống BC;AB;AC
Xét ΔBKH vuông tại K và ΔBIH vuông tại I có
BH chung
\(\widehat{KBH}=\widehat{IBH}\)
Do đó: ΔBKH=ΔBIH
=>IH=IK
Xét ΔCIH vuông tại I và ΔCEH vuông tại E có
CH chung
\(\widehat{ICH}=\widehat{ECH}\)
Do đó: ΔCIH=ΔCEH
=>HI=EH
mà HI=HK
nên HK=HE
Xét ΔAKH vuông tại K và ΔAEH vuông tại E có
AH chung
HK=HE
Do đó: ΔAKH=ΔAEH
=>\(\widehat{KAH}=\widehat{EAH}\)
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
Vậy: hai tia phân giác của hai góc ngoài của tam giác và tia phân giác của góc trong không kề với nhau đồng quy tại một điểm và giao điểm đó cách đều ba cạnh của tam giác














