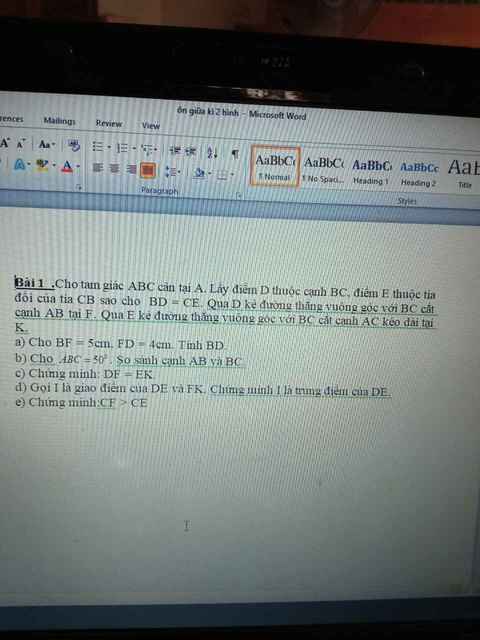
a: ΔBFD vuông tại D
=>\(DB^2+DF^2=BF^2\)
=>\(DB^2=5^2-4^2=9\)
=>\(DB=\sqrt{9}=3\left(cm\right)\)
b: Ta có: ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=180^0-2\cdot50^0=80^0\)
Xét ΔABC có \(\widehat{BAC}>\widehat{ABC}\)
mà BC,AC lần lượt là cạnh đối diện của các góc BAC;ABC
nên BC>AC
mà AC=AB
nên BC>AB
c: Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ACB}=\widehat{KCE}\)(hai góc đối đỉnh)
Do đó: \(\widehat{FBD}=\widehat{KCE}\)
Xét ΔFBD vuông tại D và ΔKCE vuông tại E có
BD=CE
\(\widehat{FBD}=\widehat{KCE}\)
Do đó: ΔFBD=ΔKCE
=>DF=EK
d: Xét ΔIDF vuông tại D và ΔIEK vuông tại E có
DF=EK
\(\widehat{IFD}=\widehat{IKE}\)(hai góc so le trong, DF//EK)
Do đó: ΔIDF=ΔIEK
=>ID=IE
=>I là trung điểm của DE