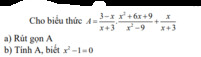\(a,A=\dfrac{3-x}{x+3}.\dfrac{x^2+6x+9}{x^2-9}+\dfrac{x}{x+3}\\ =\dfrac{-\left(x-3\right)^2}{\left(x-3\right)\left(x+3\right)}.\dfrac{\left(x+3\right)^2}{\left(x-3\right)\left(x+3\right)}+\dfrac{x}{x+3}\\ =-1+\dfrac{x}{x+3}\\ =\dfrac{-\left(x+3\right)+x}{x+3}\\ =\dfrac{-x-3+x}{x+3}\\ =\dfrac{-3}{x+3}\)
b,\(x^2-1=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
Thay x=-1 vào A ta có: \(A=\dfrac{-3}{x+3}=\dfrac{-3}{-1+3}=\dfrac{-3}{2}\)
Thay x=1 vào A ta có:\(A=\dfrac{-3}{x+3}=\dfrac{-3}{1+3}=\dfrac{-3}{4}\)
\(A=\dfrac{3-x}{x+3}.\dfrac{x^2+6x+9}{x^2-9}+\dfrac{x}{x+3}\left(x\ne3;-3\right).\\ A=\dfrac{-\left(x-3\right)}{x+3}.\dfrac{\left(x+3\right)^2}{\left(x-3\right)\left(x+3\right)}+\dfrac{x}{x+3}.\\ A=\left(-1\right)+\dfrac{x}{x+3}.\\ A=\dfrac{-x-3+x}{x+3}=\dfrac{-3}{x+3}.\)
\(x^2-1=0.\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1.\\x=-1.\end{matrix}\right.\) (TM).
\(TH1:x=1.\Rightarrow A=\dfrac{-3}{1+3}=\dfrac{-3}{4}.\\ TH2:x=-1.\Rightarrow A=\dfrac{-3}{-1+3}=\dfrac{-3}{2}.\)