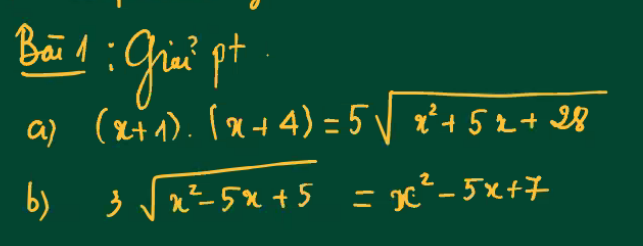b: Đặt \(\sqrt{x^2-5x+5}=a\left(a>=0\right)\)
Theo đề, ta có phương trình:
\(3a=a^2+2\)
\(\Leftrightarrow\left(a-1\right)\left(a-2\right)=0\)
=>a=1 hoặc a=2
\(\Leftrightarrow\left[{}\begin{matrix}x^2-5x+5=1\\x^2-5x+5=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)\left(x-4\right)=0\\x^2-5x+1=0\end{matrix}\right.\)
hay \(x\in\left\{1;4;\dfrac{5+\sqrt{21}}{2};\dfrac{5-\sqrt{21}}{2}\right\}\)