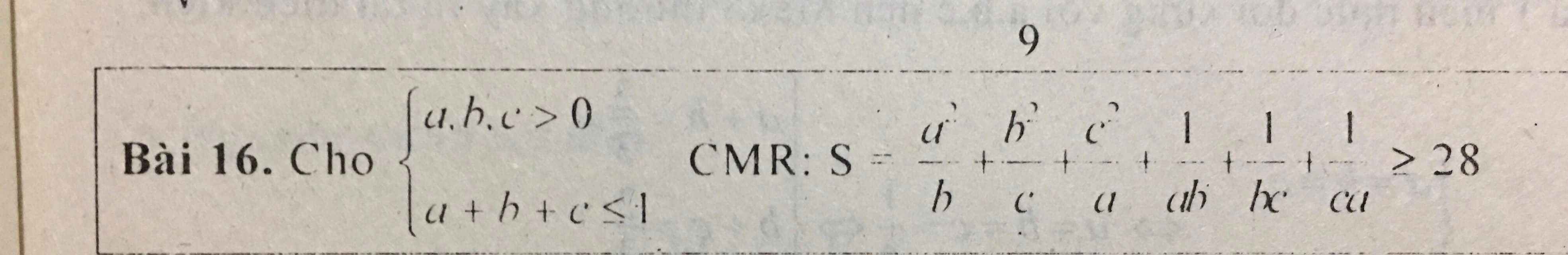\(S\ge\dfrac{\left(a+b+c\right)^2}{a+b+c}+\dfrac{9}{ab+bc+ca}=a+b+c+\dfrac{9}{ab+bc+ca}\)
\(ab+bc+ca\le\dfrac{\left(a+b+c\right)^2}{3}\)
\(\Rightarrow S\ge a+b+c+\dfrac{27}{\left(a+b+c\right)^2}=a+b+c+\dfrac{1}{\left(a+b+c\right)^2}+\dfrac{26}{\left(a+b+c\right)^2}\ge\dfrac{2}{\sqrt{a+b+c}}+26\ge2+26=28\)
xác định a,b để đường thẳng y=ax+b đi qua đi qua A(-2;3) và vuông góc với đường thẳng y=2x-5
Cho cos α = 1 3 . Tính giá trị của biểu thức P = sin 3 a - sin a sin 2 a
Cho ba số thực dương a, b, c thoả mãn \(\frac{a^5}{b+c}+\frac{b^5}{a+c}+\frac{c^5}{a+b}=\frac{3}{2}\)
Tìm max của biểu thức \(Q=ab^2+bc^2+ca^2\)
Phương trình đường thẳng đi qua hai điểm A(1; -3) và B( 2; 5) là:
A. 8x+y -5= 0
B. x+ 8y- 6= 0
C. 8x –y-11=0
D. Đáp án khác.
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip (E) có độ dài trục lớn bằng 12 và độ dài trục bé bằng 6. Phương trình
nào sau đây là phương trình của elip (E) .
A. x 2 144 + y 2 36 = 1
B. x 2 9 + y 2 36 = 1
C. x 2 36 + y 2 9 = 1
D. x 2 144 + y 2 36 = 0
Tập nghiệm của bất phương trình 2 x + 2 > 3 ( 2 - x ) + 1 là:
A. S = 1 ; + ∞
B. S = - ∞ ; - 5
C. S = 5 ; + ∞
D. S = - ∞ ; 5
Cho điểm A(-2; 1) và hai đường thẳng d1: 3x - 4y + 5 = 0 và d2: mx + 3y - 3 = 0. Giá trị của m để khoảng cách từ A đến d1 gấp hai lần khoảng cách từ A đến đường thẳng d2 là:
A. m = ± 1
B. m = ± 15 3
C. m = ± 4
D. m = ± 15 5
Phương trình (có tham số p) p p - 2 x = p 2 - 4 có nghiệm duy nhất khi
A. p ≠ 0
B. p ≠ 2
C. p ≠ ± 2
D. p ≠ 0 và p ≠ 2
Cho đường thẳng ∆ có một vectơ chỉ phương là u → - 3 ; 5 . Vectơ nào dưới đây không phải là VTCP của ∆?
A, u 1 → 3 ; − 5
B. u 2 → − 6 ; 10
C. u 3 → − 1 ; 5 3
D. u 4 → 5 ; 3
