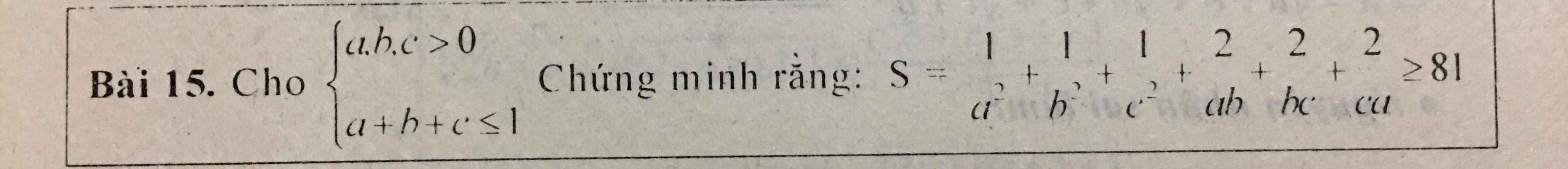Ta có:
\(S=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+2\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)\)
\(S\ge\dfrac{9}{a^2+b^2+c^2}+2.\dfrac{9}{ab+bc+ca}\)
\(S\ge9\left(\dfrac{1}{a^2+b^2+c^2}+\dfrac{1}{ab+bc+ca}+\dfrac{1}{ab+bc+ca}\right)\)
\(S\ge9.\dfrac{9}{a^2+b^2+c^2+ab+bc+ca+ab+bc+ca}=\dfrac{81}{\left(a+b+c\right)^2}\ge\dfrac{81}{1^2}=81\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
Đúng 2
Bình luận (0)
