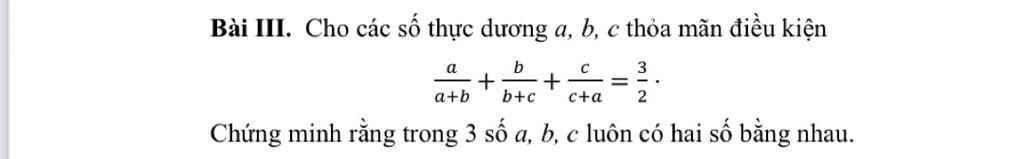Question

Answer 1

Đẳng thức ban đầu tương đương với: 

$\frac{a^2}{a^2+ab}+\frac{b^2}{b^2+bc}+\frac{c^2}{c^2+ca}=\frac{3}{2}$

Đồng thời ta có: 

$\frac{a^2}{a^2+ab}+\frac{b^2}{b^2+bc}+\frac{c^2}{c^2+ca} \ge \frac{(a+b+c)^2}{a^2+b^2+c^2+ab+bc+ca}\ge \frac{3(ab+bc+ca)}{2(ab+bc+ca)}=\frac{3}{2}$

Ta đã sử dụng bất đẳng thức: $\left\{\begin{matrix} (a+b+c)^2 \ge 3(ab+bc+ca) & \\ a^2+b^2+c^2 \ge ab+bc+ca& \end{matrix}\right.$

Dấu $"="$ xảy ra khi $a=b=c$

Do đó trong 3 số $a,b,c$ luôn tồn tại $2$ số bằng nhau