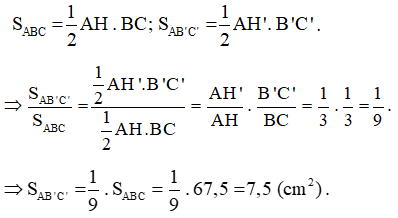a) Xét \(\Delta ABC:B'C'//BC\left(gt\right).\)
\(\Rightarrow\dfrac{B'C'}{BC}=\dfrac{AB'}{AB}\left(Talet\right)\left(1\right).\)
Xét \(\Delta ABH:B'H'//BH\left(gt\right).\)
\(\Rightarrow\dfrac{AB'}{AB}=\dfrac{AH'}{AH}\left(Talet\right)\left(2\right).\)
Từ (1) và (2) \(\Rightarrow\dfrac{AH'}{AH}=\dfrac{B'C'}{BC}\left(=\dfrac{AB'}{AB}\right).\)
b) Ta có: \(\dfrac{AH'}{AH}=\dfrac{B'C'}{BC}\left(cmt\right).\)
\(\Rightarrow B'C'=\dfrac{AH'.BC}{AH}=\dfrac{\dfrac{1}{3}AH.BC}{AH}=\dfrac{1}{3}BC.\)
\(S_{\Delta ABC}=\dfrac{1}{2}.AH.BC=67,5\left(cm^2\right).\\ S_{\Delta AB'C'}=\dfrac{1}{2}.AH'.B'C'=\dfrac{1}{2}.\dfrac{1}{3}.AH.\dfrac{1}{3}.BC=\dfrac{1}{18}.AH.BC.\)
\(\Rightarrow\dfrac{1}{9}S_{\Delta ABC}=S_{\Delta AB'C'}\Rightarrow S_{\Delta AB'C'}=7,5\left(cm^2\right).\)
a) Xét ΔABC có B'C' // BC (B' ∈ AB; C' ∈ AC)
⇒ 
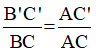(hệ quả của định lý Ta – let) (1)
Xét ΔAHC có H'C' // HC (H' ∈ AH, C' ∈ AC)
⇒ 
(định lý Ta – lét) (2)
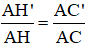
Từ (1) và (2) suy ra: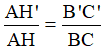 
.
b) Vì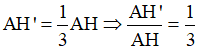 
.
Mà theo câu a, ta có: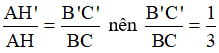 
.
Ta có:
Vậy diện tích tam giác A'B'C' là 7,5 cm2.
