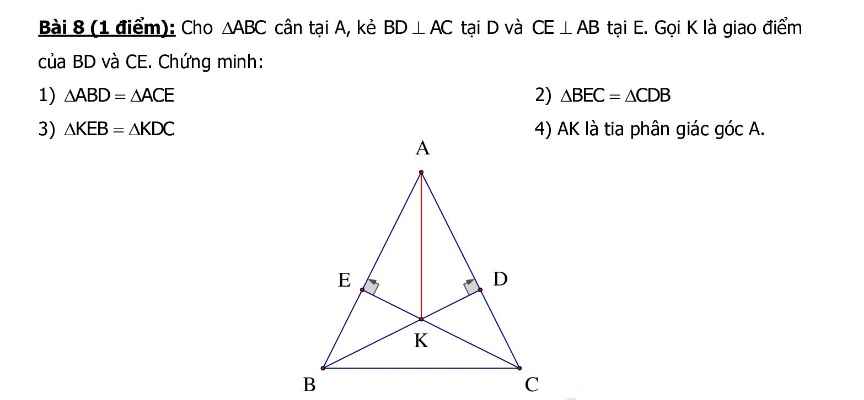
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
2: Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
CB chung
CE=BD
Do đó: ΔBEC=ΔCDB
3: Xét ΔKEB vuông tại E và ΔKDC vuông tại D có
EB=DC
\(\widehat{EBK}=\widehat{DCK}\)
Do đó: ΔKEB=ΔKDC
4: Xét ΔABK và ΔACK có
AB=AC
AK chung
BK=CK
Do đó: ΔABK=ΔACK
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)
hay AK là tia phân giác của góc BAC
1, Xét tam giác ABD và tam giác ACE có :
AB = AC (gt) ; ^ADB = ^AEC = 900
Vậy tam giác ABD = tam giác ACE ( ch - gn )
2, Xét tam giác BEC và tam giác CDB có :
^BEC = ^CDB = 900 ^EBC = ^DCB BC chung
Vậy tam giác BEC = tam giác CDB ( ch - gn )
=> BE = DC ( 2 cạnh tương ứng )
3, Xét tam giác KEB và tam giác KDC có :
^EKB = ^DKC ( đ.đ) ; ^KEB = ^KDC = 900 ; BE = DC ( cmt )
Vậy tam giác KEB = tam giác KDC (g.c.g)
4, Vì CE ; BD là đường cao
=> CE giao BD tại K
=> AK là đường cao thứ 3
mà tam giác ABC cân tại A => AK đồng thời là đường phân giác