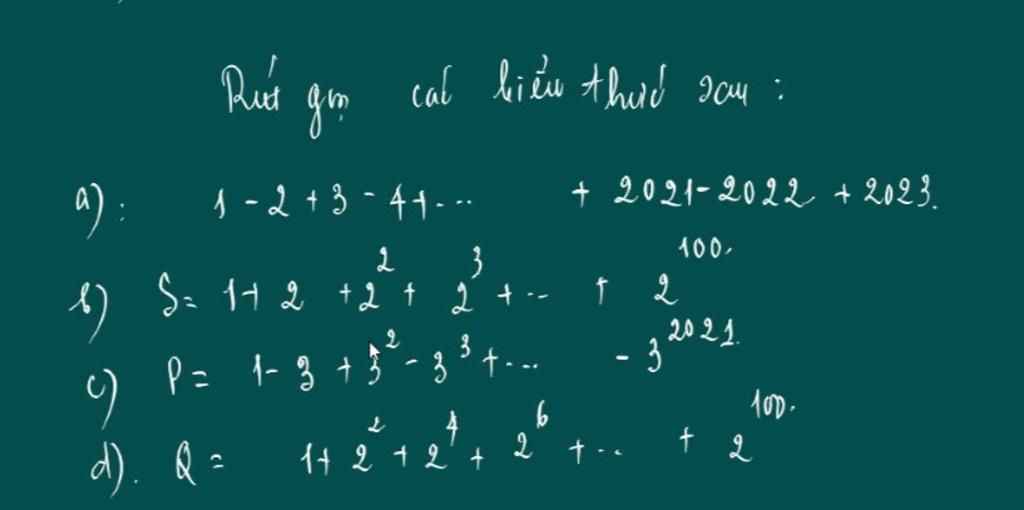b: \(2S=2+2^2+...+2^{101}\)
nên \(S=2^{101}-1\)
\(a,=-1-1-1-...-1+2023\)
Tổng có \(\dfrac{2022-1+1}{2}=1011\) số hạng \(-1\)
Vậy tổng là \(\left(-1\right)\cdot1011+2023=2023-1011=1012\)
\(b,\Rightarrow2S=2+2^2+...+2^{101}\\ \Rightarrow2S-S=2+2^2+...+2^{101}-1-2-...-2^{100}\\ \Rightarrow S=2^{101}-1\\ c,\Rightarrow3P=3-3^2+3^3-...-3^{2022}\\ \Rightarrow3P+P=1-3+3^2-...-3^{2021}+3-3^2+3^3-...-3^{2022}\\ \Rightarrow4P=3^{2022}+1\\ \Rightarrow P=\dfrac{3^{2022}+1}{4}\)
\(d,\Rightarrow4Q=2^2+2^4+...+2^{102}\\ \Rightarrow4Q-Q=2^2+2^4+...+2^{102}-1-2^2-...-2^{100}\\ \Rightarrow3Q=2^{102}-1\\ \Rightarrow Q=\dfrac{2^{102}-1}{3}\)